
Musterlösungen, Übersicht und Links
Musterlösungen

Berufskolleg Mitte - Essen


|
Autoelektrik ( Startseite) Musterlösungen, Übersicht und LinksMusterlösungen |
 Berufskolleg Mitte - Essen |

|
| vorige Seite | 4.04 mögliche Aufgaben in der Abschlussprüfung |
nächste Seite |
1. Aufgabe |
2. Aufgabe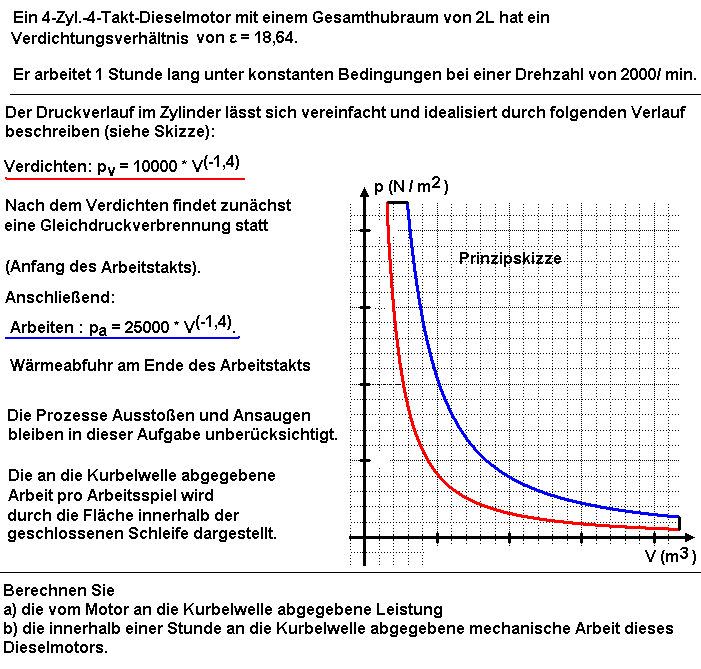 |
3. Aufgabe |
4. Aufgabe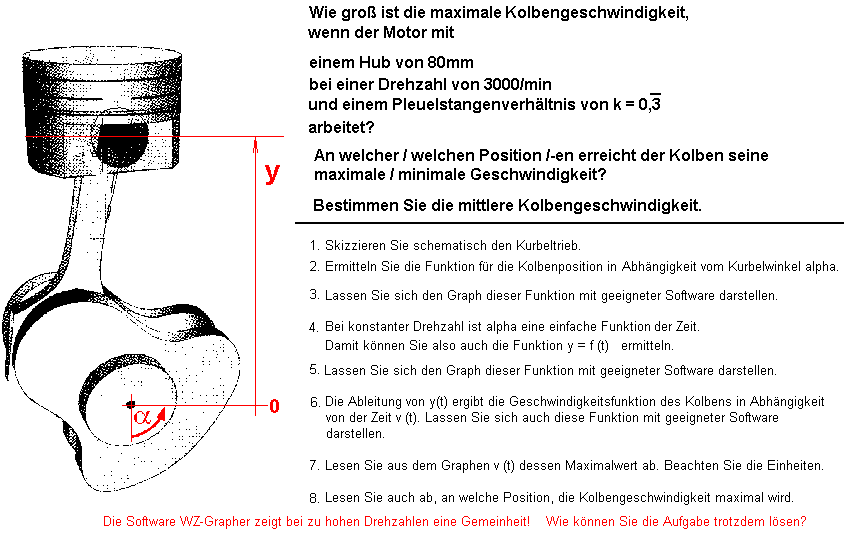 |
5. Aufgabe |
6. Aufgabe |
7. Aufgabe |
8. Aufgabe |
9. Aufgabe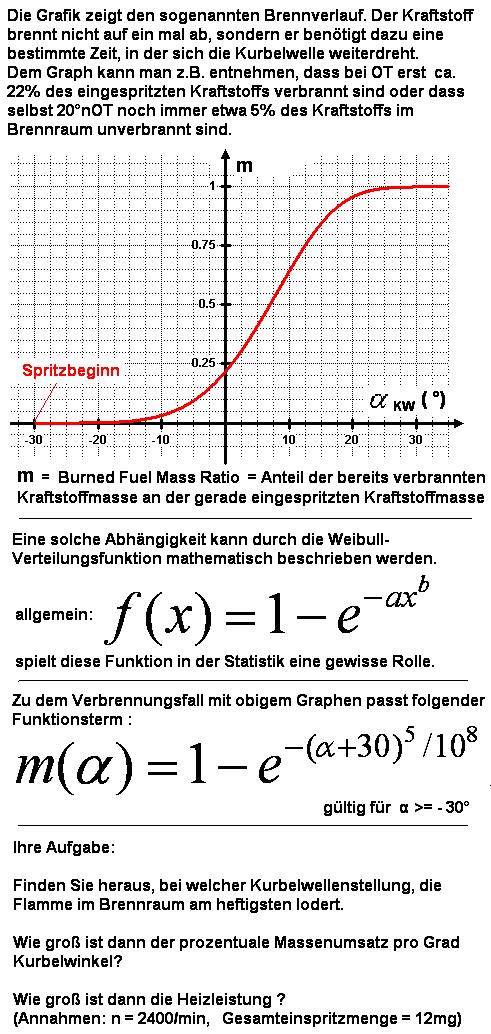 |
10. Aufgabe |
11. Aufgabe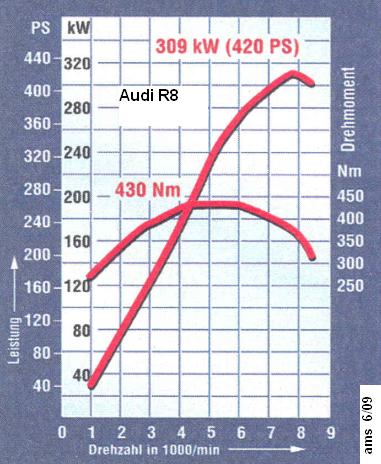 In einem Testbereicht der Zeitung "auto motor sport" konnte man die Motorkennlinien des Audi R8 finden, wie sie links abgebildet sind.
In einem Testbereicht der Zeitung "auto motor sport" konnte man die Motorkennlinien des Audi R8 finden, wie sie links abgebildet sind.Bestimmen Sie mit Hilfe der Koordinaten für das maximale Drehmoment und der maximalen Leistung je eine ganzrationale Funktion, die ... ... einen möglichst kleinen Grad haben, ... den Verlauf beider Graphen annähernd beschreiben und ... in den Extremwerten exakt mit den gegebenen Werten übereinstimen. Beachten Sie auch den mathematisch / physikalischen Zusammenhang zwischen M, n und P. Lösungshinweis |
12. AufgabeEin Radfahrer fährt auf einer bergigen Strecke. Auf einer Bergkuppe macht er Rast. Während der ersten zwei Minuten nach dieser Rast verhält sich seine Geschwindigkeit gemäß der Funktion:v(t) = 0,0001 t3 - 0,02 t2 + 1,05t Aufgaben1. Wie viele Sekunden nach Pausenende zeigt der Tacho die Höchstgeschwindigkeit an?2. Welche Maximalgeschwindigkeit erreicht der Radfahrer in der betrachteten Zeitspanne. 3. Wann und wie groß war die maximale Beschleunigung? 4. Wann und wie groß war die maximale Verzögerung? 5. Wie viele Meter konnte der Radfahrer die Beschleunigung genießen? 6. Wie lange benötigt der Radfahrer für den 1. Kilometer nach der Pause? Lösung: Aufgabe zu Weg-Zeit-Geschwindigkeit- Beschleunigung |
13. AufgabeEin Fahrzeug wird auf einer Rennstrecke aus dem Stand kurz stark beschleunigt und wieder bis zum Stillstand abgebremst.In den ersten 20s. der Fahrt verhält sich dabei die Geschwindigkeit gemäß der Funktion: v(t) = 0,007*(t - 20)2 * t2Es gelten hierbei die SI-Einheiten, die der Übersichtlichkeit wegen nicht mitgeschrieben sind.A: Welches ist die Höchstgeschwindigkeit, die das Fahrzeug ereicht? B: Wie groß ist die höchste Beschleunigung? c: Welche Strecke legt das Fahrzeug in diesen 20s. zurück? C1: mit TR C2: ohne TR D: Zeichnen Sie die 3 Graphen s(t), v(t) und a(t). Lösung: Beschleunigung - Abbremsung |
14. Aufgabe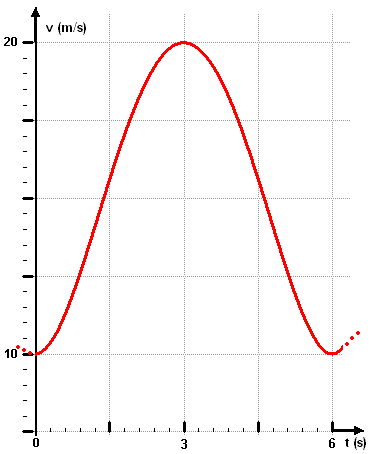 Auf einer Teilstrecke einer Achterbahn bewegt sich der Wagen so, wie der Funktionsgraf zeigt.
Auf einer Teilstrecke einer Achterbahn bewegt sich der Wagen so, wie der Funktionsgraf zeigt. A: Wie groß ist die höchste Beschleunigung? B: Wie groß ist die maximale Verzögerung? C: Welche Strecke legt das Fahrzeug in diesen 6s zurück? C1: mit TR C2: ohne TR D: Zeichnen Sie die 3 Graphen s(t), v(t) und a(t). StandardLösung: Achterbahn Lösung mit Pfiff: Achterbahn Lösung mit Sinusfunktion: Achterbahn |
15. AufgabeAufgabensatz, ähnlich wie in einer Abschlussklausur
|
16. AufgabeEin Werkzeugschlitten wird auf einer Führung periodisch hin und her bewegt.Während einer Periode erfolgt die Geschwindigkeit des Schlittens gemäß der Funktion: v(t) = 0,05*t*(t4 -12t2 +20)(alle Einheiten gemäß SI)Dabei gilt diese Geschwindigkeitsfunktion zwischen ihren beiden äußeren Nullstellen. gesucht ist: 1. Extremwerte der Geschwindigkeit 2. Extremwerte der Beschleunigung 3. gesamte während einer Stunde pausenlosen Betriebs zurückgelegte Wegstrecke Lösungen (zu Ihrer Kontrolle): vE1 = 2,01 m/s bei tE1= -2,57s vE2 = -0,51 m/s bei tE1= -0,78s vE3 = 0,51 m/s bei tE1= 0,78s vE4 = -2,01 m/s bei tE1= 2,57s aE5 = -2,24 m/s^2 bei tE5 =-1,90s aE6 = 1,00 m/s^2 bei tE6 = 0,00s aE7 = 2,24 m/s^2 bei tE7 = 1,90s s = 5,20 m Gesamtweg während einer Periode sges= 3603 m Gesamtweg in einer Stunde |
17. Aufgabegegeben ist die Funktionf(x) = 2x3 - 8x3 + 12gesucht sind die beiden Funktionsterme der Halbkreise, die gemeinsam den Vollkreis ergeben, der den Graph von f(x) in seinem Wendepunkt von links berührt und einen Durchmesser von 8 (Einheiten) hat.Die ist ganz schön harter Tobak!! Ohne Skizze bleibt die Aufgabe vermutlich für die meisten Schülerinnen und Schüler unverständlich. Also : - Skizzieren Sie ein Koordinatensystem - Tragen Sie den Graph einer Funktion 3. Grades ein. - Markieren Sie den Wendepunkt (WP). - Skizzieren Sie dann einen Kreis so, dass er den Wendepunkt von f(x) von links berührt. Wenn´s beim 1. Versuch auch nicht gleich klappt, spätestens beim 4. Anlauf, sollten Sie diese Skizze einigermaßen ordentlich auf dem Papier haben. - Markieren Sie den Mittelpunkt des Kreises (M). - Skizzieren Sie die horizontalen Durchmesserlinie des Kreises. - bezeichnen Sie den oberen Halbkreis mit fo(x). - bezeichnen Sie den unteren Halbkreis mit fu(x). - Zeichnen Sie nun noch die Gerade ein, die durch den M und WP geht. Nun haben Sie bereits eine (hoffentlich) saubere und lesbare Planskizze, an der Sie die Verhältnisse anschaulich studieren können. Wie soll´s nun weitergehen? Teillösungen zu Ihrer Kontrolle 1. Bestimmen Sie die Koordinaten des Wendepunkts. WP (4/3 ; 68/27) 2. Da der Kreis den Funktionsgraphen im Wendepunkt berühren soll, muss er dort die gleiche Steigung haben wie f(x). f´(4/3) = -32/3 3. Der Kreismittelpunkt muss auf der Geraden liegen, die senkrecht auf der Wendetangente steht. 4. Bestimmen Sie die Steigung dieser Geraden. m = 3/32 5. Bestimmen Sie die Funktionsgleichung g(x) der Geraden durch den M und WP. (Punkt u. Steigung der Geraden sind gegeben) g(x) = 3/32x + 2,39... 6. Da der Durchmesser des Kreises 8 sein soll, muss M 4 Einheiten von WP auf g(x) liegen. 7. Nun liegt also ein Problem der linearen Funktionen vor. Diese Nebenrechnung wird hier durchgeführt. 8. Der Punkt M (-2,6492; 2,1416) liegt links von Punkt W auf der Geraden g und hat von W den Abstand 4. 9. Die allgemeine Gleichung eines Kreises mit Radius a und Mittelpunkt (xM; yM) heißt: 10. (x - xm)2 + (y - ym)2 = a2 11. Diese Gleichung muss nach y umgestellt werden. Und es müssen 2 Funktionen gebildet werden, eine davon mit der positiven Wurzel und die andere mit der negatven Wurzel. 12. Auf diese Weise hat man jeweils eine Funktion für den oberen Halbkreis : yo(x) = Wurzel (16 - (x + 2,6492)2 ) + 2,1416 13. und eine Funktion für den unteren Halbkreis : yu(x) = - Wurzel (16 - (x + 2,6492)2 ) + 2,1416 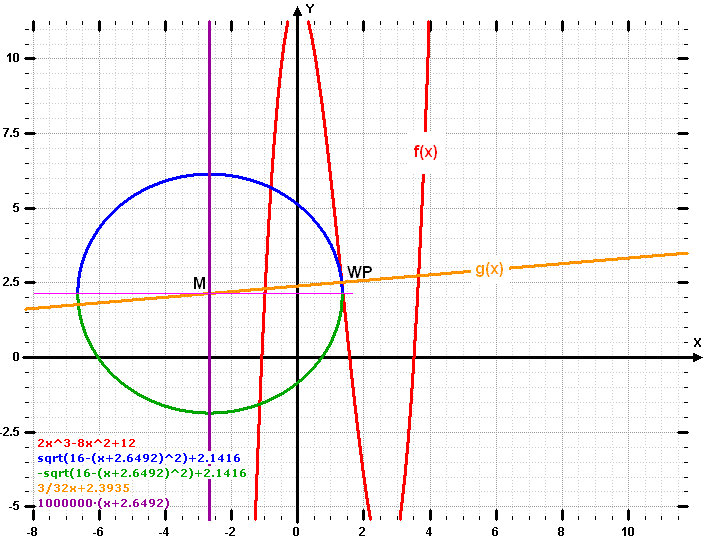
|
18. AufgabeEin Kraftfahrzeug startet bei t=0 (s) und seine Geschwindigkeit folgt der Funktionv(t) = 0,00003 * t2 * (t-30)2 * (t+10)Hierbei gilt: [t]=s, [v]= m/sBestimmen Sie:
Hinweis: Es gilt: ds(t)/dt = v(t) und dv(t)/dt = a(t) Lösungen (zu Ihrer Kontrolle):
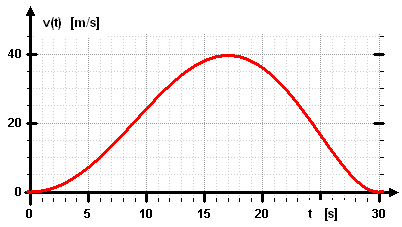 v(t) = 0,00003 * (t5 - 50t4 + 300t3 + 9000t2)
v(t) = 0,00003 * (t5 - 50t4 + 300t3 + 9000t2)
|
19. Aufgabe |
| www.kszofingen.ch | interaktive Mathetests | www.mathe-online.at | www.ies.co.jp | engl. Mathe-Java-Applets | mathenexus.zum.de | www.arndt-bruenner.de | mathematik.zum.de | www.tutorvista.com | kostenpflichtige Nachhilfe weltweit jederzeit | www.geogebra.org | kostenloses Mathe-tool (Algebra, Analysis Geometrie) | www.WolframAlpha.com | Alles was berechenbar ist, will diese Maschine (demnächst) berechnen können |
 |
vorige Seite nächste Seite |
 email an Autor |
Musterlösungen, Übersicht und Links |
 Autoelektrik Startseite |
 Berufskolleg Mitte - Essen |