	Autoelektrik ( Startseite) Musterlösungen, übersicht und Links Musterlösungen	Berufskolleg Mitte - Essen
vorige Seite	4.043 mögliche Aufgabe zur FHR-Prüfung (Achterbahn) zuletzt bearbeitet am 16.09.2010	nächste Seite

14. Aufgabe

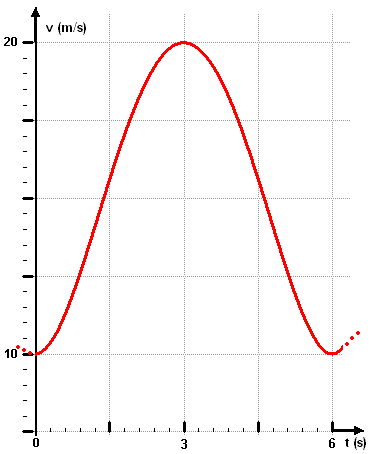Auf einer Teilstrecke einer Achterbahn bewegt sich der Wagen so, wie der Funktionsgraf zeigt.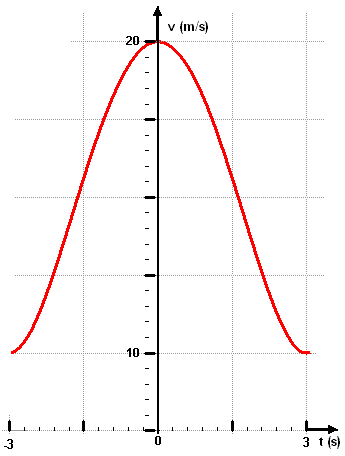

A: Wie groß ist die höchste Beschleunigung?
B: Wie groß ist die maximale Verzögerung?
C: Welche Strecke legt das Fahrzeug in diesen 6s zurück?
C1: mit TR
C2: ohne TR
D: Zeichnen Sie die 3 Graphen s(t), v(t) und a(t).

Diese Aufgaben lassen sich nur dann beantworten, wenn man den Funktionsterm kennt, der zu dem gegebenen Grafen passt.
Denn es gilt, dass die Beschleunigungsfunktion gleich der Ableitung der Geschwindigkeitsfunktion nach der Zeit ist.
Außerdem gilt, dass die zurückgelegte Strecke in der Zeit zwischen t1 und t2 gleich dem bestimmten Integral der Funktion v(t) mit den Grenzen t1 und t2 ist.

Zunächst soll noch folgende Vorüberlegung zur Vereinfachung des Problems gemacht werden: Der Funktionsgraf ist achssymmetrisch. Die Symmetrieachse ist jedoch nicht die y-Achse sondern die Achse t = 3.
. Würde man den Grafen so weit nach links verschieben, dass die y-Achse die Symmetrieachse ist, verliefe der betrachtete Teil der Achterbahnfahrt von t = -3s bis t = 3s.
Die Beschleunigungswerte und die zurückgelegte Strecke verändert sich durch die Verschiebung nicht.
Die Berechnung wird durch diese Verschiebung allerdings vereinfacht.

Der einfachste Funktionstyp, dier einen solchen Grafen erzeugt ist eine ganzrationale Funktion 4. Grades.
Wegen der Achssymmetrie kommen nur gerade Exponenten bei der unabhängig Variablen vor. Also:
Funktionsgraf v(t+3), Achterbahn

v(t) = a t⁴ +b t² + c .

Die Koeffizienten a, b und c sind zu ermitteln.

Da c der y-Achsabschnitt ist, gilt somit :

c = 20 .

Zur Bestimmung der beiden anderen Koeffizienten a und b müssen nun geeignete Gleichungen aufgestellt werden.
Diese lassen sich aber aus dem Grafen einfach konstruieren.
z.B. liegt bei t = 3 ein Extremwert von v vor, d.h. die 1. Ableitung von v(t) nach t ist bei t = 3s Null:

v '(3) = 0

Gl.I: 108a + 6b = 0

Außerdem gilt für t = 3s:

v(3) = 10

Gl.II: 81a +9b = -10

Die beiden Gleichungen (I und II) haben als Lösungen:

a = 0,1235 u. b = - 2,222

Damit heißt schließlich der gesuchte Funktionsterm für v(t):

v(t) = 0,1235 t⁴ - 2,222 t² + 20

Den Originalfunktionsterm mit der Symmetrieachse bei t=3 erhält man nun übrigens einfach, indem man im Term v(t) alle Variablen t durch (t-3) ersetzt (Verschiebung des Grafen um 3 Einheiten nach rechts!).

A: Wie groß ist die höchste Beschleunigung?

Die Beschleunigungsfunktion ist die Ableitung der Geschwindigkeitsfunktion nach der Zeit, also:

a(t) = v' (t) = 0,4938t³ - 4,444t

Um die maximale Beschleunigung zu berechnen, ist diese Funktion nun abzuleiten und = 0 zu setzen:

a' (t) = 1,481t² - 4,444 = 0

mit den Lösungen:

t1 = -1,732s und t2 = 1,732s

Auch dieses Ergebnis ist wieder so schön symmetrisch, wie es sein muss.
Den Wert der maximalen Beschleunigung erhält man durch Einsetzen der beiden Zeiten t1 und t2 in den Funktionsterm a(t). Damit ergibt sich:

a(t1) = 5,13 und a(t2) = -5,13

Der positive Wert ist die maximale Beschleunigung, der negative die maximale Verzögerung.
Die Einheiten sind bei den Berechnungen nicht mit geschleppt worden. Da aber alles im SI stattfindet, so muss es sich bei der Beschleunigung ebenfalls um den zugehörigen SI-Wert handeln, als a_max = 5,13m/s^2.
Diese Beschleunigungen liegen etwa beim halben Wert der Erdbschleunigung. Die Beschleunigung ändert sich aber innerhalb weniger Sekunden von + 5,13m/s^2auf -5,13m/s^2 und wird die FAhrgäste kräftig durchschÜtteln. Besser Sie schnallen sich vor der Fahrt an.

Bleibt noch die während der betrachteten 6 s zurückgelegte Strecke zu berechnen.
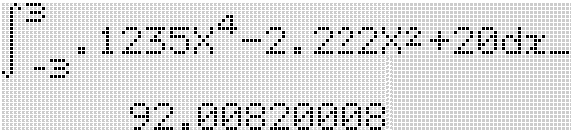
Integral01 Taschenrechneranzeige

Mit dem Taschenrechner ist dies schnell erledigt und dient zur Kontrolle des später zu Fuß berechneten Ergebnisses:

s = 92m

Zu Fuß berechnet:

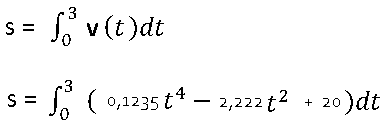Integral01

Da es sich um eine symmetrische Funktion handelt, reicht es den halben Weg (z.B. während der Bremsphase) zu berechnen und diesen dann zu verdoppeln.
Diese Überlegung vereinfacht das Verfahren wieder etwas.
Der halbe Weg ist aber gleich dem Wert des bestimmten Integrals von v(t) dt in den Grenzen von 0s bis 3s:

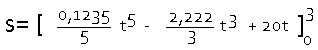Integral01

Nun freut man sich über die Vereinfachung: untere Grenze = 0.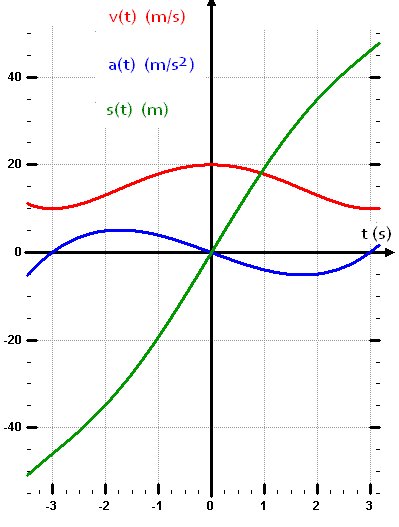
Setzt man also die obere Grenze bei t ein, so erhält man auch hier:

s/2 = 46m => s = 92m

Zeichnen der Grafen:
Graphen a(t), v(t) s(t)

Hier sind einige Links zu finden, die zu interessanten / hilfreichen Matheseiten im WWW führen.

www.kszofingen.ch	interaktive Mathetests
www.mathe-online.at
www.ies.co.jp	engl. Mathe-Java-Applets
mathenexus.zum.de
www.arndt-bruenner.de
mathematik.zum.de
www.tutorvista.com	kostenpflichtige Nachhilfe weltweit jederzeit
www.geogebra.org	kostenloses Mathe-tool (Algebra, Analysis Geometrie)
www.WolframAlpha.com	Alles was berechenbar ist, will diese Maschine (demnächst) berechnen können