Grundlagen der Elektrotechnik

	Autoelektrik ( Startseite) Musterlösungen, übersicht und Links Musterlösungen	Berufskolleg Mitte - Essen
vorige Seite	4.042 mögliche Aufgabe zur FHR-Prüfung (Beschleunigung - Verzögerung) zuletzt bearbeitet am 03.06.2010	nächste Seite

Aufgabe

Ein Fahrzeug wird auf einer Rennstrecke aus dem Stand kurz stark beschleunigt und wieder bis zum Stillstand abgebremst.
In den ersten 20s. der Fahrt verhält sich dabei die Geschwindigkeit gemäß der Funktion:

v(t) = 0,007(t - 20)² t²

Es gelten hierbei die SI-Einheiten, die der übersichtlichkeit wegen nicht mitgeschrieben sind.

A: Welches ist die Höchstgeschwindigkeit, die das Fahrzeug ereicht?
B: Wie groß ist die höchste Beschleunigung?
c: Welche Strecke legt das Fahrzeug in diesen 20s. zurück?
C1: mit TR C2: ohne TR D: Zeichnen Sie die 3 Graphen s(t), v(t) und a(t).

Aufgabe

A: Welches ist die Höchstgeschwindigkeit, die das Fahrzeug ereicht?

Setzt man die Ableitung von v(t) Null, so erhält man die Zeitpunkte, an denen die Extremwerte der Geschwindigkeit erreicht werden.
Setzt man diese Zeitpunkte jeweils in die Funktion v(t) ein, so erhält man die Extremwerte der Geschwindigkeit.

v(t) = 0,007(t - 20)² t²

nach Ausmultiplizieren ergibt sich:

v(t) = 0,007t⁴ - 0,28t³ + 2,8t²

v' (t) = 0,028t³ - 0,84t² + 5,6t

0,028t³ - 0,84t² + 5,6t = 0

Es ergeben sich die Zeiten:

t₁ = 10 und t₂ = 20

t₁ und t₂ eingesetzt in v(t):

v(10) = 0,00110⁴ - 0,0410³ + 0,4*10² = 70 (m/s= 252km/h)

v(20) = 0,00120⁴ - 0,0420³ + 0,4*20² = 0 (m/s)

Das Fahrzeug erreicht also nach 10s seine maximale Geschwindigkeit von 252 km/h und kommt nach nach weiteren 10s wieder zum Stillstand.

B: Wie groß ist die höchste Beschleunigung?

Die Beschleunigungsfunktion ist die Ableitung der Geschwindigkeitsfunktion nach der Zeit, also:

a(t) = v' (t) = 0,028t³ - 0,84t² + 5,6t (s.o.)

a(t) = 0,028t³ - 0,84t² + 5,6t

Will man die maximale Beschleunigeung berechnen, muss man die Ableitung der Beschleunigungsfunktion Null setzen.
Dann erhält man alle Zeitpunkte, wo die Beschleunigung ihre Extremwerte hat.
Setzt man diese Zeiten dann in a(t) ein, erhält man die zugehörigen extremen Beschleunigungswerte.

a' (t) = 0,084t² - 1,68t +5,6 = 0

0,084t² - 1,68t + 5,6 = 0

Es ergeben sich die Zeiten:

t₃ = 4,226 und t₄ = 15,77

t₁ und t₂ eingesetzt in a(t):

a(t) = 0,028 * 4,226³ - 0,84 * 4,226² + 5,6 * 4,226 = 10,78 (m/s)

a(t) = 0,028 * 15,77³ - 0,84 * 15,77² + 5,6 * 15,77 = -10,77 (m/s)

Maximale Verzögerung und maximale Beschleunigung sind also während dieser Fahrt gleich groß.

c: Welche Strecke legt das Fahrzeug in diesen 20s. zurück?

Die zurückgelegte Strecke erhält man, wenn man die Fläche unter dem Funktionsgraphen v(t) zwischen t= 0 und t = 20s berechnet.
Es ist also das bestimmte Integral
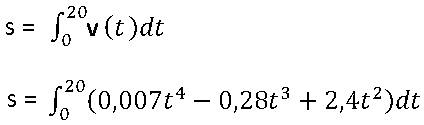
Integral01

zu lösen.

s= (0,0014 * 20⁵ - 0,07 * 20⁴ + 0,8 * 20³)

s= 746,7 (m)

D: Zeichnen Sie die 3 Graphen s(t), v(t) und a(t).

Die Merkmale der 3 Graphen ermittelt man nach den Regeln der Kurvendiskussion.
Hier werden nur die Ergebnisse tabellarisch zusammengefasst.

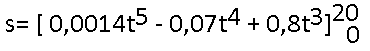
t (s)	v(t) (m/s)	a(t) (m/s²	s(t) (m)	Bemerkungen
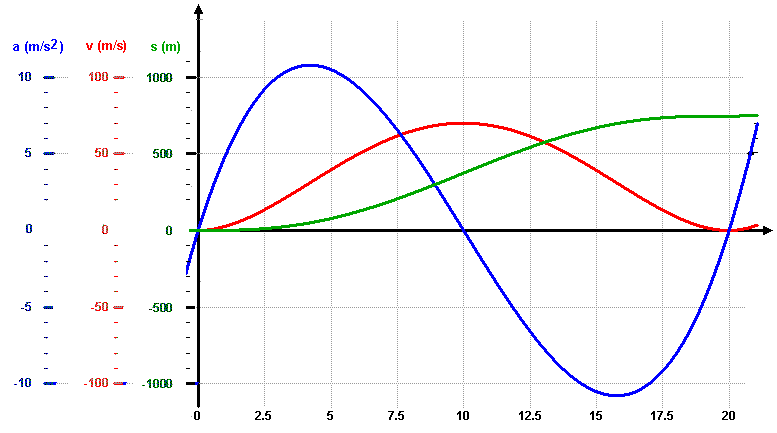
0	0	0	0	Start der Fahrt
4,226	31	10,8	50	max. Beschleunigung, Wendepunkt von v(t)
10	70	0	373	"Halbzeit", max. Geschwindigkeit, Beschleunigung = 0, Beschleunigung geht über in Verzögerung, halber Weg zurückgelegt
15,77	31	-10,8	696	max. Verzögerung Wendepunkt von v(t)
20	0	0	746	Ende der Fahrt
	achssymmetrisch, Symmetrieachse: x=10	punktsymmetrisch, Symmetriepunkt: (10;0)	punktsymmetrisch, Symmetriepunkt: (10; 373)

Hier sind einige Links zu finden, die zu interessanten / hilfreichen Matheseiten im WWW führen.

www.kszofingen.ch	interaktive Mathetests
www.mathe-online.at
www.ies.co.jp	engl. Mathe-Java-Applets
mathenexus.zum.de
www.arndt-bruenner.de
mathematik.zum.de
www.tutorvista.com	kostenpflichtige Nachhilfe weltweit jederzeit
www.geogebra.org	kostenloses Mathe-tool (Algebra, Analysis Geometrie)
www.WolframAlpha.com	Alles was berechenbar ist, will diese Maschine (demnächst) berechnen können

Musterlösungen

4.042 mögliche Aufgabe zur FHR-Prüfung (Beschleunigung - Verzögerung)

Aufgabe

v(t) = 0,007*(t - 20)2 * t2

Aufgabe

v(t) = 0,007*(t - 20)2 * t2

v(t) = 0,007t4 - 0,28t3 + 2,8t2

v' (t) = 0,028t3 - 0,84t2 + 5,6t

0,028t3 - 0,84t2 + 5,6t = 0

t1 = 10 und t2 = 20

v(10) = 0,001*104 - 0,04*103 + 0,4*102 = 70 (m/s= 252km/h)

v(20) = 0,001*204 - 0,04*203 + 0,4*202 = 0 (m/s)

a(t) = v' (t) = 0,028t3 - 0,84t2 + 5,6t (s.o.)

a(t) = 0,028t3 - 0,84t2 + 5,6t

a' (t) = 0,084t2 - 1,68t +5,6 = 0

0,084t2 - 1,68t + 5,6 = 0

t3 = 4,226 und t4 = 15,77

a(t) = 0,028 * 4,2263 - 0,84 * 4,2262 + 5,6 * 4,226 = 10,78 (m/s)

a(t) = 0,028 * 15,773 - 0,84 * 15,772 + 5,6 * 15,77 = -10,77 (m/s)

s= (0,0014 * 205 - 0,07 * 204 + 0,8 * 203)

s= 746,7 (m)

Hier sind einige Links zu finden, die zu interessanten / hilfreichen Matheseiten im WWW führen.

v(t) = 0,007(t - 20)² t²

v(t) = 0,007(t - 20)² t²

v(t) = 0,007t⁴ - 0,28t³ + 2,8t²

v' (t) = 0,028t³ - 0,84t² + 5,6t

0,028t³ - 0,84t² + 5,6t = 0

t₁ = 10 und t₂ = 20

v(10) = 0,00110⁴ - 0,0410³ + 0,4*10² = 70 (m/s= 252km/h)

v(20) = 0,00120⁴ - 0,0420³ + 0,4*20² = 0 (m/s)

a(t) = v' (t) = 0,028t³ - 0,84t² + 5,6t (s.o.)

a(t) = 0,028t³ - 0,84t² + 5,6t

a' (t) = 0,084t² - 1,68t +5,6 = 0

0,084t² - 1,68t + 5,6 = 0

t₃ = 4,226 und t₄ = 15,77

a(t) = 0,028 * 4,226³ - 0,84 * 4,226² + 5,6 * 4,226 = 10,78 (m/s)

a(t) = 0,028 * 15,77³ - 0,84 * 15,77² + 5,6 * 15,77 = -10,77 (m/s)

s= (0,0014 * 20⁵ - 0,07 * 20⁴ + 0,8 * 20³)