	Autoelektrik ( Startseite) Musterlösungen, übersicht und Links Musterlösungen	Berufskolleg Mitte - Essen
vorige Seite	4.0432 mögliche Aufgabe zur FHR-Prüfung (Achterbahn) Lösung mit Sinusfunktion zuletzt bearbeitet am 16.09.2010	nächste Seite

14. Aufgabe

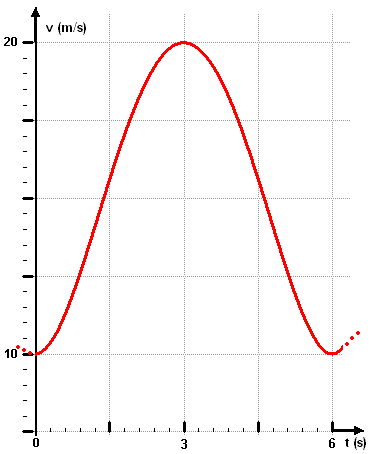Auf einer Teilstrecke einer Achterbahn bewegt sich der Wagen so, wie der Funktionsgraf zeigt.

A: Wie groß ist die höchste Beschleunigung?
B: Wie groß ist die maximale Verzögerung?
C: Welche Strecke legt das Fahrzeug in diesen 6s zurück?
C1: mit TR
C2: ohne TR
D: Zeichnen Sie die 3 Graphen s(t), v(t) und a(t).

Diese Aufgaben lassen sich nur dann beantworten, wenn man den Funktionsterm kennt, der zu dem gegebenen Grafen passt.
Denn es gilt, dass die Beschleunigungsfunktion gleich der Ableitung der Geschwindigkeitsfunktion nach der Zeit ist.
Außerdem gilt, dass die zurückgelegte Strecke in der Zeit zwischen t1 und t2 gleich dem bestimmten Integral der Funktion v(t) mit den Grenzen t1 und t2 ist.

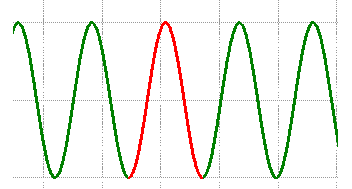Der dargestellte Graph könnte auch Teil einer Sinus-Funktion sein.

v(t) =A + B * sin(2πf*t+ φ)

Die 4 Koeffizienten A, B, f und φ sind zu ermitteln.

Der Mittelwert einer Sinusfunktion, die zwischen dem Minimum 10 und dem Maximum 20 schwingt ist natûrlich 15.
A= 15 (m/s)
B ist die Amplitude also die Schwingungsweite vom Mittelwert bis zum Maximum.
B= 5 (m/s)
f ist die Frequenz der Schwingung, also der Kehrwert der Periodendauer. Diese beträgt 6s.
f= 1/6 (Hz)
φ ist die Phasenverschiebung (Verschiebung der Sinuslinie parallel zur t-Achse). Die Phasenverscheibung beträgt hier eine Viertel Periode nach rechts.
φ = -π/2

Damit hat man den Funktionsterm fûr v(t) gefunden:

v(t) = 15 +5 * sin (2 * π * 1/6 * t - π/2)

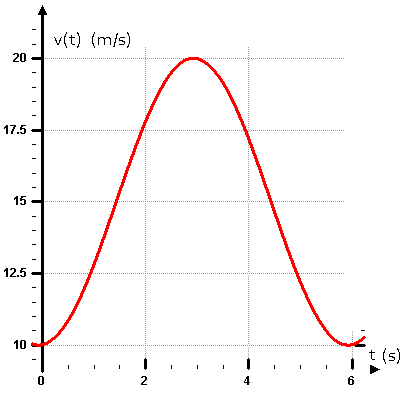und man entnimmt dem Funktionsgraf: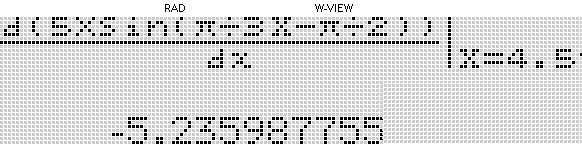
v '(-3) = 0
v '(0) = 0
v '(3) = 0

Außerdem weiß man wegen der Symmetrieeigenschaften der Sinus-Funktion, dass die
größte Steigung bei t= 1,5s und die
kleinste Steigung (größtes Gefälle) bei t= 4,5s sein mûssen.

Also kennt man bereits die Zeiten, wo die Beschleunigung jeweils maximal bzw. minimal ist.
Und man weiß, dass der Betrag der maximalen Beschleunigung gleich dem Betrag der maximalen Verzögerung ist.

A: Wie groß ist die höchste Beschleunigung?

Die Beschleunigungsfunktion ist die Ableitung der Geschwindigkeitsfunktion nach der Zeit, also:

a(t) = v' (t) = (15 +5 * sin (2 * π * 1/6 * t - π/2))'

Um die Funktion v(t) nach t ableiten zu können, muss man im Wesentlichen die Ableitung der Sinusfunktion und die Kettenregel anweden und erhält:

a(t) = 5 * cos(π /3 * t - π/2) * π/3

Da der Zeitpunkt der maximalen Beschleunigung bereits bekannt ist (t= 1,5),kann man sich nun den Aufwand sparen, a(t) abzuleiten und gleich Null zu setzen, um diesen Wert mûhsam zu erhalten.
Hier kann man also direkt a(1,5) berechnen Achtung: Taschenrechner im RAD- Winkelmodus betreiben!

a(1,5) = 5,24 (m/s²)

Zur Probe wird noch die maximale Verzögerung noch berechnet, die zur Zeit t=4,5 vorliegt:

a(4,5) = - 5,24 (m/s²)

Berechnung der Ableitung von v(t) zur Zeit t= 4,5s mit dem Taschenrechner:
TR Ergebnisdisplay amax

Im übrigen ist die maximale Beschleunigung auch mit elementaren Kenntnissen der Eigenschaften der Sinus-Funktion ganz ohne Ableitung möglich:
Die maximale Steigung hat der Graf der Sinusfunktion beim Durchgang durch die Ruhelage.
Diese beträgt bei y = sin(x) genau 1 (45°)
Die Funktion y= 5 sin(x) erscheint gegen y= sin(x) um den Faktor 5 in y-Richtung gestreckt.
Dieser Faktor ûberträgt sich auch auf die Steigung, s.d. y=5 sin(x) eine maximale Steigung von 5 hat.
Da die Periodendauer der betrachteten Funktion nicht 2π beträgt sondern 6, erhöht sich im Verhältnis 2π/6 die Steigung.
Also:

die maximale Steigung der Funktion y=5 sin(2π/6 x) beträgt 5* 2π / 6 = 5,236.

Eine Phasenverschiebung bzw. eine Verschiebung in y-Richtung ändert daran nichts.

Bleibt noch die während der betrachteten 6s zurückgelegte Strecke zu berechnen.
Der Weg ist aber gleich dem Wert des bestimmten Integrals von v(t) dt in den Grenzen von 0s bis 6s:
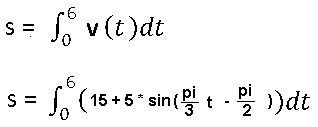
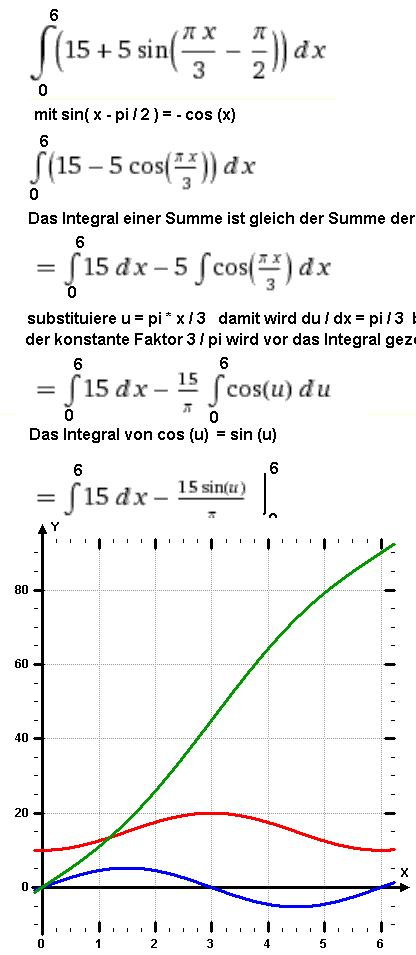
Integral01

Mit dem Taschenrechner hat man schnell berechnet:

s = 90 (m)

Zu Fuß berechnet, ergibt sich:

Integral01

So erhält man auch hier:

s = 90 (m)

zugegeben: Diese Integration ist nicht Bestandteil des Grundkurses Analysis!

Zeichnen der Grafen:
Integral01

Hier sind einige Links zu finden, die zu interessanten / hilfreichen Matheseiten im WWW führen.

www.kszofingen.ch	interaktive Mathetests
www.mathe-online.at
www.ies.co.jp	engl. Mathe-Java-Applets
mathenexus.zum.de
www.arndt-bruenner.de
mathematik.zum.de
www.tutorvista.com	kostenpflichtige Nachhilfe weltweit jederzeit
www.geogebra.org	kostenloses Mathe-tool (Algebra, Analysis Geometrie)
www.WolframAlpha.com	Alles was berechenbar ist, will diese Maschine (demnächst) berechnen können