14. Aufgabe
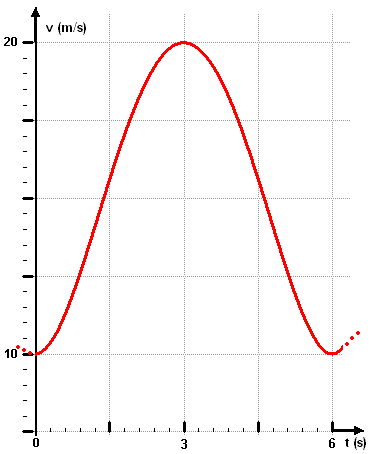Auf einer Teilstrecke einer Achterbahn bewegt sich der Wagen so, wie der Funktionsgraf zeigt.
A: Wie groß ist die höchste Beschleunigung?
B: Wie groß ist die maximale Verzögerung?
C: Welche Strecke legt das Fahrzeug in diesen 6s zurück?
C1: mit TR
C2: ohne TR
D: Zeichnen Sie die 3 Graphen s(t), v(t) und a(t).
Diese Aufgaben lassen sich nur dann beantworten, wenn man den Funktionsterm kennt, der zu dem gegebenen Grafen passt.
Denn es gilt, dass die Beschleunigungsfunktion gleich der Ableitung der Geschwindigkeitsfunktion nach der Zeit ist.
Außerdem gilt, dass die zurückgelegte Strecke in der Zeit zwischen t1 und t2 gleich dem bestimmten Integral der Funktion v(t)
mit den Grenzen t1 und t2 ist.
Der einfachste Funktionstyp, der einen solchen Grafen erzeugt, ist eine ganzrationale Funktion 4. Grades.
v(t) = a t4 +b t3 + c t2 + d t + e
Die 5 Koeffizienten a, b, c, d und e sind zu ermitteln.
Dazu sind 5 geeignete Gleichungen erforderlich. Diese erhält man aus 5 geeigneten Wertepaaren, die man aus dem Funktionsgrafen abliest.
Im Prinzip ist es egeal, welche 5 Wertepaare man aussucht, doch kann man sich durch geschickte Wahl das Leben stark vereinfachen.
Es bieten sich die 3 Extrema als Wertepaare an. Zusätzlich lassen sich dort weitere Gleichungen aus der Ableitung bilden.
1. (0 ; 10)
2. (3 ; 20)
3. (6 ; 10)
v '(t) = 4a t3 + 3b t2 + 2c t + d
und man entnimmt dem Funktionsgraf:
4. v '(0) = 0
5. v '(3) = 0
6. v '(6) = 0
So könnte man bereits 6 Gleichungen aufstellen, von denen aber (normalerweise) nur 5 nötig sind. Hier werden folgende 5 Gleichungen gebildet:
I. v(0) = a 04 + b 03 + c 02 + d 0 + e = 10
II. v(3) = a 34 + b 33 + c 32 + d 3 + e = 20
III. v'(0) = 4a 03 + 3b 02 + 2c 0 + d = 0
IV. v'(3) = 4a 33 + 3b 32 + 2c 3 + d = 0
V. v'(6) = 4a 63 + 3b 62 + 2c 6 + d = 0
oder etwas anders notiert:
I. v(0) = 0a + 0b + 0c + 0d + e = 10
II. v(3) = 81a + 27b + 9c + 3d + e = 20
III. v'(0) = 0a + 0b + 0c + d = 0
IV. v'(3) = 108a + 27b + 6c + d = 0
V. v'(6) = 864a + 108b + 12c + d = 0
Das sind 5 Gleichungen mit den 5 Unbekannten.
Aus Gl. I. ergibt sich sofort, dass e = 10 sein muss.
Aus Gl. III. ergibt sich sofort, dass d = 0 sein muss.
Wenn man dies gleich ausnutzt, bleiben die Gleichungen II., IV und V übrig:
II. v(3) = 81a + 27b + 9c + 10 = 20
IV. v'(3) = 108a + 27b + 6c = 0
V. v'(6) = 864a + 108b + 12c = 0
oder:
II. 81a + 27b + 9c = 10
IV. 108a + 27b + 6c = 0
V. 864a + 108b + 12c = 0
Es gibt Taschenrechner, die können ein solches Gleichungssystem lösen. Es ergibt sich:
a= 0,12346
b = -1,4815
c = 4,444
d = 0
e = 10
wobei d und e bereits vorher bekannt waren.
Damit lautet der Funktionsterm für v(t):
v(t) = 0,12346 t4 - 1,4815 t3 + 4,444 t2 + 10
A: Wie groß ist die höchste Beschleunigung?
Die Beschleunigungsfunktion ist die Ableitung der Geschwindigkeitsfunktion nach der Zeit, also:
a(t) = v' (t) = 0,4938 t3 - 4,444 t2 + 8,888 t
Um die maximale Beschleunigung zu berechnen, ist diese Funktion nun abzuleiten und = 0 zu setzen:
a' (t) = 1,481 t2 - 8,888 t + 8,888 = 0
Die Lösungen dieser quadratischen Gleichung sind:
t1 = 1,268
t2 = 4,734
Zu diesen beiden Zeiten hat also die Beschleunigung jeweils einen Extremwert.
Wie groß dieser ist, berechnet man durch Einsetzen von t1 und t2 in die Funktion a(t).
Dann erhält man:
a(t1) = 5,132
a(t2) = -5,129
also eine maximale Beschleunigung und eine maximale Verzögerung.
t1 und t2 müssen spiegelsymmetrisch zu t = 3s liegen.
Die Beträge von a(t1) und a(t2) müssen gleich sein.
Die Rechnung zeigt diese Symmetrie mit ausreichender Genauigkeit (Rundungen).
Die zugehörigen Einheiten sind die entsprechenden SI-Einheiten, also m, s, m/s und m/s2.
Bleibt noch die während der betrachteten 6 s zurückgelegte Strecke zu berechnen.
Der Weg ist aber gleich dem Wert des bestimmten Integrals von v(t) dt in den Grenzen von 0s bis 6s:
Mit dem Taschenrechner hat man schnell berechnet:
s = 91,97
Zu Fuß berechnet, ergibt sich:
Nun freut man sich über die untere Grenze = 0.
Setzt man also die obere Grenze bei t ein, so erhält man auch hier:
s = 91,97 (m)
Zeichnen der Grafen:
Hier sind einige Links zu finden, die zu interessanten / hilfreichen Matheseiten im WWW führen.
