3. Aufgabe
Prüfung zur Fachhochschulreife
Berufskolleg Mitte der Stadt Essen
Fach Mathematik
Schuljahr 2009 / 2010
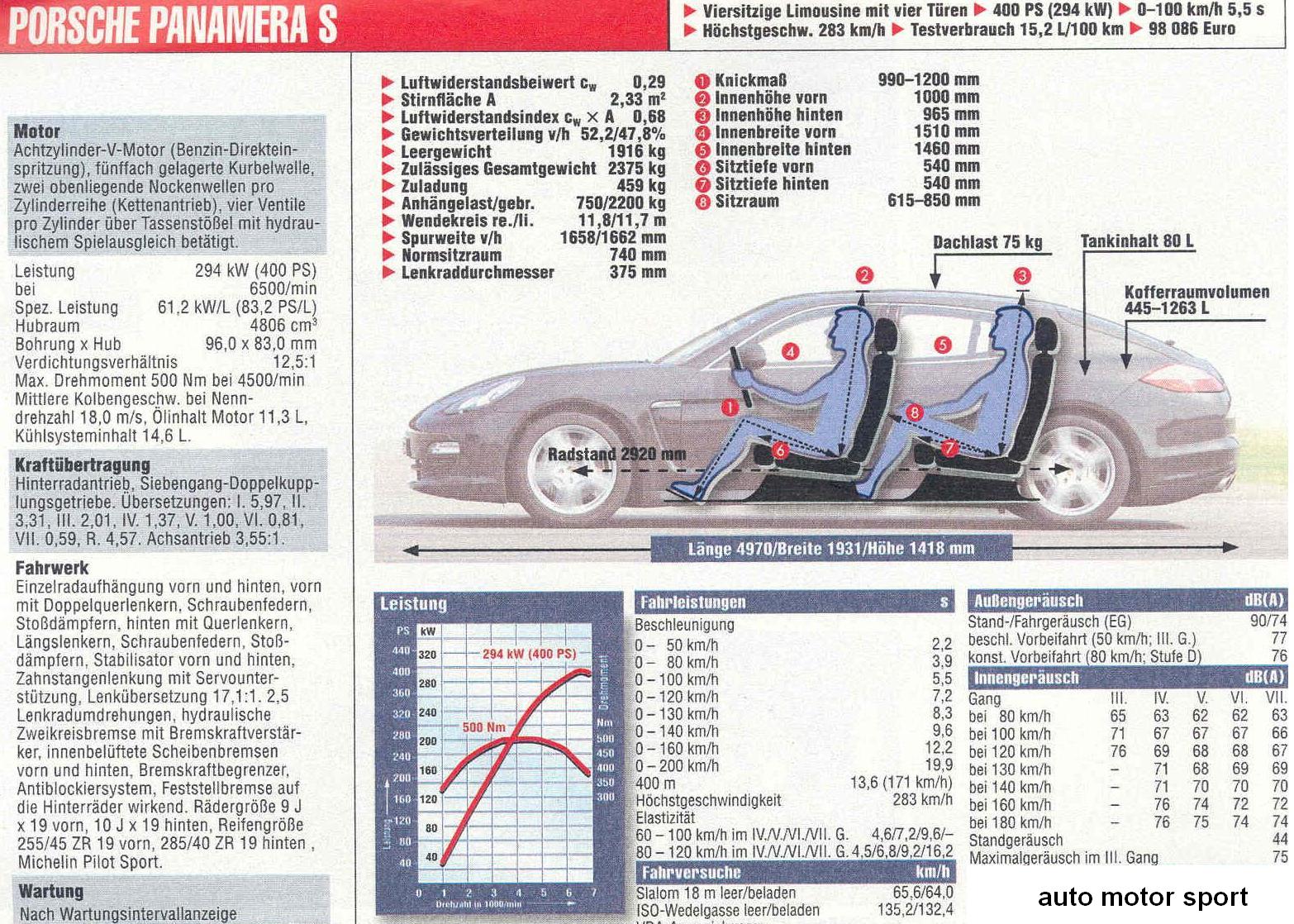
Einige Daten des Porsche Panamera S wurden in der Zeitschrift ams 18/2009, S 28 veröffentlicht (s. unten).
Aufgaben:
M1. Bestimmen Sie aus den Motorkennlinien jeweils die Wertepaare für Pmax und Mmax. 10 Pkte
M2. Ermitteln Sie für die Funktionen M(n) und P(n) jeweils einen passenden
Term einer Polynomfunktion mit folgenden Eigenschaften: 100 Pkte
* Bei Drehzahl 0/min sollen jeweils Drehmoment und Leistung 0 sein.
* Für Pmax und Mmax sollen die Funktionsterme jeweils die von Ihnen in M1.
bestimmten Werte „exakt“ berechnen.
* Der bekannte technisch-physikalische Zusammenhang zwischen P, M und n
soll natürlich für alle Drehzahlen gelten.
* Der Grad jeder Funktion soll möglichst niedrig sein.
* Der Graph jeder Funktion soll dem jeweils in der Abbildung gegebenen
Kurvenverlauf möglichst nahe kommen.
M3. Berechnen Sie die jeweiligen prozentualen Abweichungen der durch Ihre Funktionen
ermittelten Maximalwerte von P und M von den Datenblattwerten. 20 Pkte
M4. Stellen Sie die Graphen Ihrer beiden Funktionen M(n) und P(n) im Drehzahlbereich
0<= n <= 7000 dar. 20 Pkte
Hinweise
Weisen Sie nach, dass folgendes oder ein ähnliches Gleichungssystem zu lösen ist:
n1a + n1b + n1c + n1d = M1 mit n1 Drehzahl bei maximalem Moment
4n1a + 3n1b + 2n1c + d = 0 n2 Drehzahl bei maximaler Leistung
n2a + n2b + n2c + n2d = P2/f M1 maximales Moment
5n2a + 4n2b + 3n2c + 2nd = 0 P2 maximale Leistung
f 1/9550
Sollte Ihnen dieser Nachweis nicht gelingen, so lösen Sie das Gleichungssystem, um die 4 Koeffizienten a,b,c und d der Polynomfunktion für M zu ermitteln.
Nutzen Sie für die Lösung zunächst Formelzeichen.
Setzen Sie Zahlenwerte erst ein, wenn es unbedingt nötig ist (Platz- / Arbeitsersparnis und bessere Übersichtlichkeit).
Arbeiten Sie mit mindestens 4-stelliger Genauigkeit.
Hilfsmittel: Tabellenbuch / Formelsammlung KFZ (Europa-Verlag),
handgeschriebene und mit Schulstempel versehene Formelsammlung (Mathematik)
Taschenrechner (nicht grafikfähig)
Anlage Datenblatt Panamera S (ams 18/2009)
(Drehzahlangabe bei Mmax ist gegenüber dem Original verändert!)
|
4. Aufgabe
Prüfung zur Fachhochschulreife
Berufskolleg Mitte der Stadt Essen
Fach Mathematik
Schuljahr 2010 / 2011
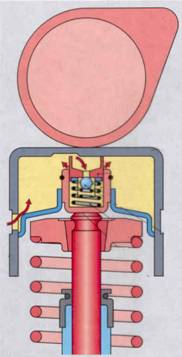
Ventiltrieb nockenbetätigt
Der Nocken eines Einlassventils hat ein solches symmetrisches Profil, dass die Ventilgeschwindigkeit beim Öffnen und Schließen nach der Funktion:
v(t) = -1,2*1017 *(t2 - (tö/2)2)2 * t3
erfolgt.
tö = 12ms (Öffnungszeit Einlassventil)
aEV =120° (Öffnungswinkel des Einlassventils auf der Nockenwelle)
m = 205g (Masse Einlassventil)
Aufgabe:
1. Ermitteln Sie die Kurbelwellendrehzahl des Otto-4-Takt-Motors.
2. Schätzen Sie die maximale Ventilgeschwindigkeit ab und begründen Sie Ihre Schätzung kurz.
3. Berechnen Sie nun die maximale Ventilgeschwindigkeit.
a) ohne Taschenrechner
b) mit Taschenrechner (zur Kontrolle)
4. Welche maximale Kraft ist bei dieser Drehzahl zur Beschleunigung des Ventils erforderlich?
5. Wie groß ist der Ventilhub?
6. Stellen Sie die 3 Funktionsgraphen v(t) (Geschwindigkeit), a(t) (Beschleunigung) und s(t) (Weg)
in einem Diagramm mit gemeinsamer t-Achse (DIN A4-Blatt Querformat) möglichst formatfüllend dar.
Zeichnen Sie in 3 verschiedenen Farben oder in 3 verschiedenen Linienarten.
Notieren Sie eine Legende, welche Farbe /Linienart für welchen Graph verwendet wurde.
Hilfsmittel: Tabellenbuch / Formelsammlung KFZ (Europa-Verlag),
handgeschriebene und mit Schulstempel versehene Formelsammlung (Mathematik)
Taschenrechner (nicht grafikfähig)
|











