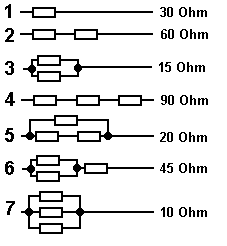
Seitenende Autoelektrik (Startseite)

Grundlagen der Elektrotechnik


Gleichstromtechnik


Gemischte Schaltungen

zuletzt bearbeitet am 30.10.2006

Valid HTML 4.01 Transitional

gemischte Schaltung 1

Beispiel 1


Knotenregel


Maschenregel


Beispiel 2


Vergleich zweier Schaltpläne


































Seitenanfang

Beispiel 1

Knotenregel






gemischte Schaltung 1 In einer Gemischten Schaltung von Widerständen kommen sowohl Reihenschaltungen als auch Parallelschaltungen gleichzeitig vor. Hat man z.B. genau drei Widerstände zur Verfügung, so zeigt die Abbildung alle Möglichkeiten, diese 3 Bauteile zu schalten. Die Schaltungen 2 und 4 sind natürlich Reihenschaltungen und Schaltungen 3 und 7 sind Parallelschaltungen. Aber Schaltungen 5 und 6 sind gemischte Schaltungen. (Mehr ist eben mit nur 3 Bauteilen nicht drin.) Die Werte rechts neben den Schaltungen geben jeweils den zugehörigen Gesamtwiderstand an, wenn alle Widerstände denselben Wert von 30 Ohm haben.

Den Wert von Schaltung 5 berechnet man, indem zunächst die beiden in Reihe geschalteten Widerstände zusammengefasst werden (30 Ohm + 30 Ohm= 60 Ohm) und anschliessend die verbleibende Parallelschaltung berechnet wird ( (60 Ohm * 30 Ohm) /( 60 Ohm + 30 Ohm) = 20 Ohm) ..

Den Wert von Schaltung 6 berechnet man nun so, dass man zunächst die beiden parallelgeschalteten Widerstände zusammenfasst ( (30 Ohm * 30 Ohm) /( 30 Ohm + 30 Ohm) = 15 Ohm) und anschliessend die verbleibende Reihenschaltung kalkuliert (15 Ohm + 30 Ohm = 45 Ohm).





















Beispiel1

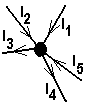Knotenregel

Maschenregel







Zur Berechnung beliebiger Schaltungen reichen im Prinzip die beiden nun folgenden relativ einfachen Kirchhoffschen Regeln. Das hört sich zunächst simpel an, kann aber im Ernstfall zu verflixten Aufgabenbandwürmern führen.


Kirchhoffsche-Regel-1 oder Knotenregel

Knoten Unter einem Knoten versteht man hier einen Stromverzweigungspunkt wo also mindestens 2 Leitungen miteinander Verbindung haben.

Für einen solchen Punkt gilt immer:



Die Summe aller Ströme ist immer gleich Null.

I1 + I2+ I3 + I4 + I 5 + ... = 0 A

In den Knoten fließt genausoviel Strom hinein, wie gleichzeitig auch wieder herausfließt..










Das ist insofern auch klar, weil ein solcher Knoten kein Elektronenspeicher ist (im Sinne von Tiefgarage), wo Elektronen beliebig geparkt werden können. Ein Knoten ist eher wie eine Straßenkreuzung, wo die oben genannten Regeln im Allgemeinen für Autos auch gelten.

Auf den gezeichneten Knoten übertragen ergibt sich, wenn man die dort vorliegenden Stromrichtungen berücksichtigt:

I1 + I2 + I5 = I3 + I4.











Knotenregel

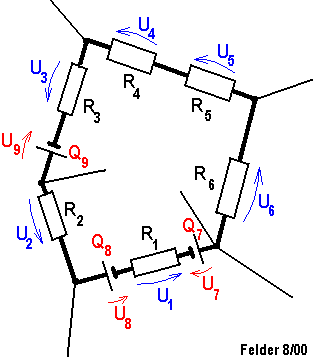Maschenregel

Beispiel 2





Kirchhoffsche-Regel-2 oder Maschenregel

Masche Unter einer Masche versteht man einen in sich geschlossenen Stromkreis der beliebige und beliebig viele elektrische Bauteile (Verbraucher oder auch Spannungsquellen) enthalten kann..

Für eine solche Masche gilt immer:

Die Summe aller Spannungen ist immer gleich Null.

U1 + U2 + U3 + ... = 0V

In einer Masche wird durch die vorhandenen Spannungsquellen immer genausoviel Spannung produziert, wie gleichzeitig auch wieder an den Verbrauchern fällt.















Dabei sind folgende übereinkünfte zu beachten:
1. Die Spannung einer Quelle ist in Richtung + Pol -> -Pol gerichtet.
2. Die Spannung einer Senke (Verbraucher) ist in Stromrichtung gerichtet.
3. Kennt man die Stromrichtung von vornherein nicht, so wählt man eine. Eine dann daraus berechneter negativer Strom bedeutet, dass die Anfangsvermutung falsch war und der Strom in die entgegengesetzte Richtung fließt.
4. Diese Regel ist unabhängig von den Bedingungen ausserhalb bzw. innerhalb der Masche. Da in der gezeichneten Masche mehrere unbekannte, entgegengesetzt gepolte Spannungsquellen vorkommen, ist die Stromrichtung unbekannt. Es wird zunächst vermutet, dass der Strom im Gegenzeigersinn fließt (blaue Pfeile an den Widerständen). So ergibt sich :

U1 + U2+ U3 + U4 + U5 + U6 + U8 - U7 - U9 = 0V











Maschenregel

Beispiel 2

Vergleich zweier Schaltpläne





Für viele Fälle reicht anstelle der allgemeinen Berechnung mit Hilfe der beiden Kirchhoffschen Regeln die einfachere Methode der schrittweisen Auflösung der Schaltung. Dies soll an folgendem Beispiel mit 7 Widerständen erläutert werden.

gegeben: R1 = 200 Ohm, R2 = 450 Ohm, R3 = 125 Ohm, R4 = 500 Ohm, R5 = 750 Ohm, R6 = 150 Ohm, R7 = 350Ohm, U0 = 12V in folgender Schaltung.

Die Aufgabe besteht darin, den Strom durch jeden Einzelwiderstand und die Spannung an jedem Einzelwiderstand zu ermitteln (vollständige Schaltungsanalyse).


1 gemischte Schaltung1 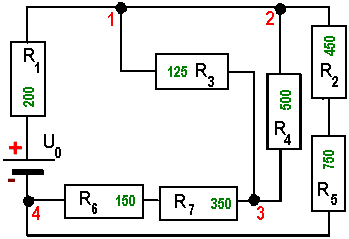Dies ist eine zunächst etwas unübersichtliche gemischte Schaltung. Durch schrittweise Zusammenfassung von je 2 Widerständen kann sie jedoch ziemlich leicht berechnet werden.

Mit etwas Übung erkennt man, dass die Widerstände R6 und R7 eine Reihenschaltung bilden und zum Widerstand R67 von 500Ohm zusammengefasst werden können. Dies ist im nächsten Bild dargestellt.

Für eine bessere Übersichtlichkeit wurde der Widerstand R3 "geradegerückt". Häufig lässt sich eine Schaltung wesentlich einfacher analysieren, wenn eine andere Darstellung gewählt wird. Dabei ergibt sich das Problem zu entscheiden, ob zwei verschiedene Schaltpläne dieselbe Schaltung darstellen!




2 gemischte Schaltung2 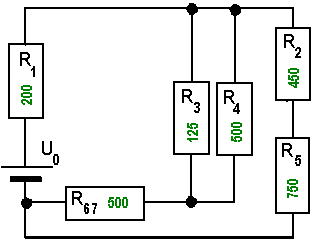Ebenso bilden die Widerstände R2 und R5 eine Reihenschaltung und werden zum Widerstand R25 von 1200 Ohm zusammengefasst, was wieder im nächsten Bild dargestellt wird. Welche beiden Widerstände nun zuerst zusammengefasst werden ist völlig egal, mit viel Übung, hätte man diese beiden Schritte auch in einem erledigen können.









3 gemischte Schaltung3 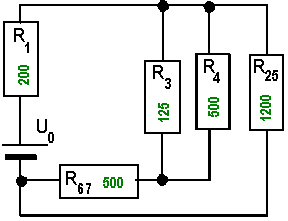Nach den beiden ersten Schritten liegt nun eine Schaltung mit nur noch 5 Widerständen vor. Man ahnt schon, dass das Verfahren so weitergeht, bis schliesslich nur noch ein Widerstand übrigbleibt.

Der nächste empfehlenswerte Schritt ist die Zusammenfassung der Widerstände R3 und R4 nach den Regeln der Parallelschaltungzu einem Widerstand R34 mit 100 Ohm, womit sich das nächste Bild ergibt.

Übrigens ist die Reihenfolge der Auflösung nicht festgelegt, sondern es gibt meist viele Möglichkeiten dies zu tun. Es gehört wieder Übung dazu, den sinnvollsten Weg möglichst schnell herauszufinden.




4 gemischte Schaltung4 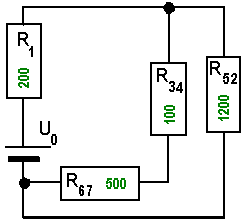Mit der abnehmenden Zahl der Bauteile, werden natürlich auch die zugehörigen Schaltpläne immer kleiner und übersichtlicher.

Jetzt werden, klar doch, die Widerstände R67 und R34 zum Widerstand R3467 vereint mit 600 Ohm Gesamtwiderstand. (siehe nächsten Schaltplan)








5 gemischte Schaltung5 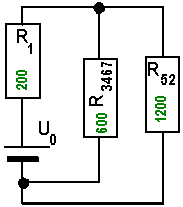Aus R3467 und R52 als Parallelschaltung wird nun der resultierende Widerstand R234567 mit 400 Ohm berechnet.

Als Grobkontrolle wenden sie den Satz an, dass in einer Parallelschaltung der Gesamtwiderstand kleiner ist als der kleinste Einzelwiderstand. Der Gesamtwiderstand muss also kleiner sein als 600 Ohm. Die Berechnung könnte also stimmen.

So erhalten Sie die fast fertige Auflösung im nächsten Plan.





6 gemischte Schaltung6 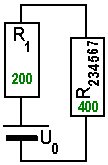Hier ist nur noch die Reihenschaltung aus R1 und R234567 mit dem Gesamtwiderstand von 600 Ohm zu berechnen. Damit ist die Schaltung maximal reduziert und wird im nächsten Bild dargestellt.









7 gemischte Schaltung 7 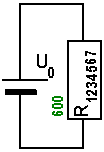Damit ist klar, dass die Spannungsquelle keinen Unterschied merkt, ob sie nun mit einem einzigen Widerstand von 600 Ohm belastet wird oder aber mit der gesamten Ausgangsschaltung. In beiden Fällen wird die Quelle gleich stark belastet, nämlich mit einem Strom von I = U / R1234567 = 12V / 600 Ohm = 0,02 A = 20mA, wie es im nächsten Bild eingetragen ist.














































































































Die bisher durchgeführten Überlegungen und Berechnungen stellen aber leider nur die halbe durchzuführende Arbeit dar, denn es geht ja um eine vollständige Schaltungsanlalyse. Es ist jetzt noch erforderlich, die bis hierhin durchgeführten Einzelschritte in umgekehrter Reihenfolge zu durchlaufen und dabei alle möglichen Einzelspannungen und Einzelströme zu berechnen.


8 gemischte Schaltung8 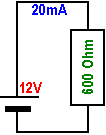Basis der weiteren Analyse ist diese Schaltung, wo alle Kenngrößen bereits ermittelt sind.
9 gemischte Schaltung9 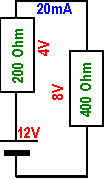Der Einzelwiderstand aus Bild 8 wird aufgeteilt in eine Reihenschaltung aus zwei Widerständen mit den Werten aus Bild 6. Mit dem Ohmschen Gesetz und den Regeln für die Reihenschaltung lassen sich die in Bild 9 angegebenen Teilspannungen berechnen:
U1 = R1 * I1 = 200 Ohm * 20 mA = 4V
U234567 = R234567 * I234567 = 400 Ohm * 20 mA = 8V
Als Probe muss gelten U1+U2=Uges,
4V + 8V =12V.
Am größeren Widerstand fällt, wie von den Regeln gefordert, auch tatsächlich die größere Spannung.

Natürlich lassen sich diese Ergebnisse auch auf anderen Rechenwegen finden.
10 gemischte Schaltung10 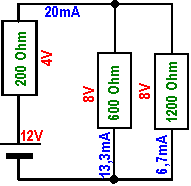In diesem Schritt wird der 600 Ohm Widerstand in die Parallelschaltung aus Bild 5 zerlegt. Nun sind selbstverständlich das Ohmschen Gesetz und die Regeln der Parallelschaltung bzw die Knotenregel zu beachten, um die Teilströme zu ermitteln. Am oberen Verzweigungspunkt teilt sich der Strom von insgesamt 20mA auf in die beiden Teilströme. Diese vereinigen sich am unteren Verzweigungspunkt wieder zum Gesamtstrom von 20mA. Von vorneherein ist klar, dass die Teilströme nicht gleich groß sein können, da die beiden Widerstände unterschiedlich sind, aber als Parallelschaltung an derselben Spannung liegen. Durch den kleineren Widerstand fließt der größere Strom! Ohne zu rechnen kann man sogar feststellen, dass durch den kleineren Widerstand doppelt so viel Strom fliessen muss wie durch den größeren, denn der größere Widerstand ist schliesslich doppelt so groß wie der kleinere.
Die Rechnungen :
I3467 = U3467 / R3467 = 8V / 600 Ohm = 13,3mA

I25 = U25 / R25 = 8V / 1200 Ohm = 6,7mA

(Als Probe muss gelten I25+I3467=Iges

13,3mA + 6,7mA =20mA.)

bestätigen diese überlegungen.
11 gemischte Schaltung11 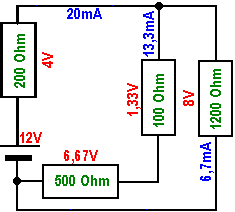So geht die Berechnung ihren Weg, bis die Schaltung wieder in allen Details vorliegt.Das ist nicht besonders schwierig, kann aber bei großen Schaltungen erheblichen Aufwand bedeuten.

Hier wird der Widerstand R3467 in eine Reihe der beiden Teilwiderstände R34 und R67 zerlegt, wie man im Bild 5 nachschauen kann. Die überlegungen hier sind völlig analog zu denen in Bild 9 und führen zu den angegebenen Ergebnissen.

Wer zu faul ist, nachzurechnen sollte wenigstens die zwei Kriterien der Reihenschaltung prüfen:
1. ist die Summe der Einzelspannungen gleich der Gesamtspannung?
2.liegt der größere Widerstand auch an der größeren Teilspannung?

Hier sind beide Kriterien erfüllt. Das allein ist zwar noch kein ausreichender Beweis für die Richtigkeit der Rechnung, aber umgekehrt gilt: Ist eins der beiden Kriterien nicht erfüllt oder sogar beide, dann ist die Berechnung garantiert falsch.
12 gemischte Schaltung12 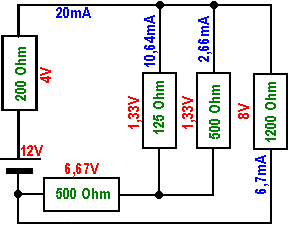Nun sind alle Überlegungen zur Schaltungsanalyse soweit bekannt. Vergleichen Sie die Schaltung 12 mit Schaltung 3. Dann wissen Sie, welche weiteren Zerlegungen hier stattgefunden haben. Die Berechnungen sind analog denen in Bild 10.

Die Schnellprobe hier funktioniert nach den beiden Kriterien für die Parallelschaltung:
1. ist die Summe der Einzelströme gleich dem Gesamtstrom?
2. fließt durch den größeren Widerstand auch der kleinere Teilstrom?
13 gemischte Schaltung13 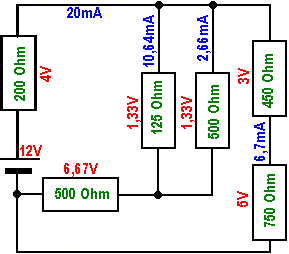analog Bild 8
14 gemischte Schaltung14 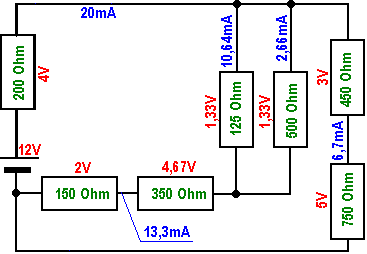Endlich liegt die komplette Ausgangsschaltung aus Bild1 wieder detailiert vor. (Der Widerstand 3 ist etwas anders eingezeichnet.) An den Bauteilen sind nun alle Einzelströme und -spannungen ablesbar. Damit ist diese Schaltung vollständig analysiert und die Aufgabe ist gelöst.

Ist eigentlich an allen Knoten hier die Knotenregel und an allen Maschen die Maschenregel erfüllt?













































































































Und was hat das alles mit der Kfz-Elektrik zu tun? Einige Aufgaben, von denen manche allerdings über das Berufsschulniveau hinausgehen, sind im Aufgabenteil gestellt.













Beispiel 2

Vergleich zweier Schaltpläne

Seitenende








A gemischte Schaltung 1 Schaltpläne gemischte Schaltung geben nicht die räumliche Anordnung der einzelnen Komponenten wider, wie das z.B. technische Zeichnungen im Maschinenbau oder in der Architektur tun, sondern zeigen nur die Stromflussmöglichkeiten.

Daher kann man ein und dieselbe Schaltung in vielen verschiedenen Plänen widergeben, hier wird z.B. eine Schaltung durch die beiden gezeigten Pläne A und B dargestellt.

Im Folgenden soll nachgewiesen werden, dass beide Pläne dieselbe Schaltung darstellen:
B 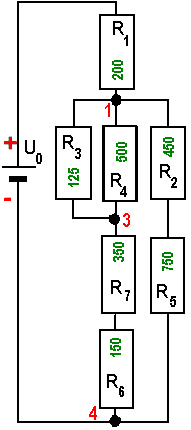gemischte Schaltung 1 in aufgelöster Darstellung Vergleichen Sie die Einzelkomponenten in beiden Schaltungen miteinander:
Gibt es in Schaltung A dieselben Spannungsquellen wie in B?
Gibt es in Schaltung A dieselben Widerstände (Anzahl und Werte) wie in B?
Gibt es in Schaltung A dieselben sonstigen Bauteile (Kondensatoren, Dioden, Spulen, Transistoren, Lampen, Relais, ...(Anzahl und Werte) wie in B?

In Plan A gibt es offenbar vier Verzeigungspunkte in Plan B aber nur 3!!
Da aber zwischen den Punkten 1 und 2 in Plan A eine direkte elektrische Verbindung besteht, können diese beiden Punkte auch zu einem (in Plan B Punkt 1) zusammengefasst werden.

Soweit haben also beide Pläne dieselben Eigenschaften. Nun muss allerdings noch die Verbindungen in beiden Schaltungen überprüft werden:
In beiden Schaltungen:
* liegt zwischen Akku + und Verzweigungspunkt 1 der Widerstand R1.

* liegen zwischen Verzweigungspukt 1 und 3 die beiden Widerstände R3 und R4 parallel.

* liegen zwischen Verzweigungspukt 3 und 4 die beiden Widerstände R6 und R7 in Reihe.

* liegen zwischen Verzweigungspukt 1 (=Verzweigungspunkt 2 in Plan A) und Verzweigungspunkt 4 die beiden Widerstände R2 und R5 in Reihe.

* sind Akku - und Verzweigungspunkt 4 direkt miteinander verbunden.

Da dieser vollständige Vergleich stets Übereinstimmung gezeigt hat, ist erwiesen, dass beide Pläne dieselbe Schaltung darstellen.











































Die hier vorgeführte Strategie zur Analyse einer gemischten Schaltung funktioniert nicht allgemein, d.h. es gibt Schaltungen, bei denen dieses Verfahren nicht zum Ziel führt.

Allgemein lässt sich aber jede Schaltung analysieren, indem man aus dem Ohm´schen Gesetz, der Knotenregel und der Maschenregel ein geeignetes(!) Gleichungssystem zusammenstellt und dieses dann auflöst.

Demonstrationen dieses Verfahrens findet man in den Kapiteln Berechnung der Ströme und Spannungen in einer Startanalage.
Berechnung einer gemischten Schaltung 1.
Berechnung einer gemischten Schaltung 2.
Berechnung einer Brückenschaltung.
















Seitenanfang Quickstart eMail an Autor Startseite zurückblättern vorblättern Stichwortverzeichnis Aufgaben Seite:

14