Grundlagen der Elektrotechnik
Gleichstromtechnik
Parallelschaltung von Widerständen
zuletzt bearbeitet am 09.10.03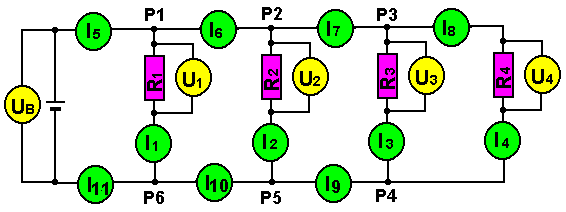
|
Autoelektrik (Startseite) Grundlagen der ElektrotechnikGleichstromtechnikParallelschaltung von Widerständenzuletzt bearbeitet am 09.10.03 |

|
|
|
Darstellung u. Messwerte in der Parallelschaltung |
|
 |
Sie sehen links eine elektrische Parallelschaltungaus:
Die Messgeräte sind nur zum Zweck der Forschung und Lehre eingebaut. Sie gehören normalerweise nicht zur Schaltung. |
|
Eigenschaften u. Formeln |
|
Alle Widerstände liegen zur selben Zeit an derselben Spannung (hier Batteriespannung). |
UB = U1 = U2 = U3 = U4 (= U5 =...) |
|
Wichtig ist auch die Gleichzeitigkeit. Zu anderen Zeiten haben sich evtl. manche Bedingungen für die Schaltung geändert (z.B. die Bordnetzspannung) Dann liegen natürlich die Widerstände an einer anderen Spannung, jedoch sehen auch dann alle gleichzeitig wieder dieselbe neue Spannung. Diese Betrachtung stimmt übrigens dann nicht mehr, wenn die Leitungen Widerstände haben (aber dann liegt auch eine gemischte Schaltung vor, die anders berechnet werden muss.) | Diese Formel lässt sich so beliebig erweitern. |
Die Ströme durch die Einzelwiderstände addieren sich zum Gesamtstrom |
I5 = I1 + I2 + I3 * I4 (+ I5 + ...) |
|
An den Verzweigungsstellen P1, P2, P3 ... teilt sich der Strom wie der Autostrom an einer Strassenkreuzung. Der Gesamtstrom kommt aus der Spannungsquelle (hier I5) bzw. fliesst auch wieder in die Spannungsquelle zurück (hier I11). Im allgemeinen gilt die Kirchhoffsche Regel: In einen Knotenpunkt (Verzweigungspunkt) fliesst genau so viel Strom hinein, wie gleichzeitig auch wieder herausfliesst. (In eine Strassenkreuzung ...) | Auch diese Formel lässt sich beliebig erweitern. |
Fällt ein Verbraucher aus, merken die übrigen Verbraucher davon nichts. | |
| Bei dieser Behauptung vernachlässigt man den Innenwiderstand einer Spannungsquelle. Man tut so, als habe man eine ideale Spannungsquelle, die ihre Spannung konstant hält, egal wie stark sie belastet wird. | |
Die Ströme durch die Einzelwiderstände verhalten sich zueinander umgekehrt proportional wie die zugehörigen Widerstandswerte. | I1 / I2 = R2 / R1 oder |
|
Je grösser der Widerstand in einer solchen Schaltung, desto weniger Strom fliesst durch ihn. Ist z.B. ein Widerstand 10mal so gross wie sein Parallelwiderstand, so fliesst durch ihn nur ein 10tel des Stromes. In einer Parallelschaltung mit 2 gleichgrossen Widerständen fliesst durch jeden Einzelwiderstand genau der halbe Gesamtstrom Mit einer Parallelschasltung kann man einen Gesamtstrom in beliebige Teilströme aufteilen. Dazu muss man nur die passenden Widerstände auswählen: Stromteiler | |
In einer Parallelschaltung addieren sich die Kehrwerte aller Einzelwiderstände zum Kehrwert des Gesamtwiderstands | 1 = 1/R1 + 1/R2 + 1/R3 + 1/R4 (+ 1/R5 + ...) |
|
Diese Formel ist wesentlich komplizierter als alle vorher genannten. Beachten Sie die Bruchrechenregeln. Die Zusammenhänge lassen sich einfacher erklären, wenn man den Leitwert nutzt. | oder Rg = 1 / (1/R1 + 1/R2 + 1/R3 + 1/ R4 (+ 1/ R5 + ...)) Diese Formeln sind beliebig erweiterbar. |
In einer Parallelschaltung addieren sich die Einzelleitwerte zum Gesamtleitwert | Gg = G1 + G2 + G3 + G4 (+ G5 + ...) |
| Bei der Parallelschaltung spielen die Leitwerte dieselbe Rolle wie bei der Reihenschaltung die Widerstände. | |
In einer Parallelschaltung ist der Gesamtwiderstand immer kleiner als der kleinste Einzelwiderstand. | |
|
Eine Abschätzung des Gesamtwiderstands einer Parallelschaltung nach dieser Aussage reicht manchmal, wenn man die Eigenschaften der Schaltung sich
überlegen will. Rg ist eben immer kleiner als jeder Einzelwiderstand, insbesondere also auch kleiner als der kleinste Einzelwiderstand. |
|
Beispiele aus der Kfz-Technik |
|
 |
Quickstart |  |
 |
 |
 |
 |
Seite:13 |