Beispielberechnung 1

zuletzt bearbeitet am 19.11.2004

Berechnung einer gemischten Schaltung 1

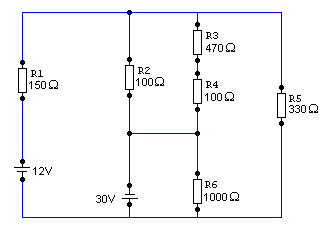
	Gegeben ist die abgebildete Schaltung aus 2 Spannungsquellen und 6 Widerst�nden mit den Werten aller Widerst�nde und den Spannungswerten der beiden Akkus. Zu berechnen sind alle Einzelspannungen an den Widerst�nden und alle Einzelstr�me, die irgendwie in dieser Schaltung messbar sind.
Als Werkzeuge stehen zur Verf�gung:	- das Ohm�sche Gesetz (U = R * I), - die Knotenregel (Die Summe aller in einen Knoten hineinflie�enden Str�me ist gleich der Summe aller aus dem Knoten abflie�enden Str�me. bzw.: Die Summe aller Str�me in einem Knoten = 0A. ), sowie - die Maschenregel ( Die Summe aller Spannungen beim Umlauf um eine Masche ist 0V.) Es soll gezeigt werden, wie man mit diesen Hilfsmitteln eine solche Schaltung analysieren kann.
	Zun�chst werden in die Schaltung alle Einzelspannungen und Einzelstr�me eingetragen. Dabei ist zu beachten: Die Strompfeile werden in der mutma�lichen Richtung eingetragen. Ist die Stromrichtung unbekannt, so entscheide man sich beliebig f�r eine Richtung. Die Spannungspfeile an Spannungsquellen zeigen vom Pluspol zum Minuspol. Die Spannungspfeile an Verbrauchern (Widerst�nden) zeigen in Stromrichtung. Mit diesen Regeln erh�lt man z.B. die linke Abbildung.
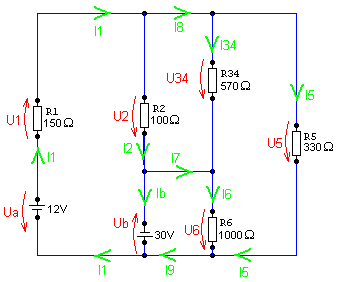	Die Widerst�nde R3 und R4 werden zun�chst zu einem Ersatzwiderstand R34 zusammengefasst. R34 = R3 + R4 (Reihenschaltung) Au�erdem ist klar, dass Ia = I1 sein muss, weil zwischen Ia und I1 Strom weder ab- noch zuflie�en kann. Damit wird der Plan etwas einfacher:
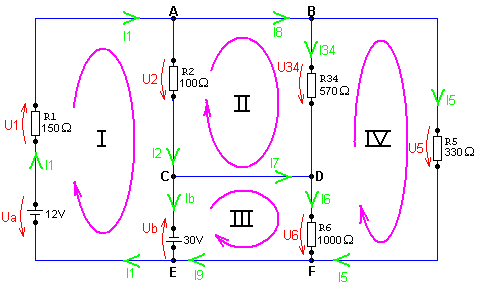	Bevor man Formeln aufstellen und mit der Rechnung beginnen kann, muss man sich noch f�r die Umlaufrichtung in jeder einzelnen Maschen entscheiden. Au�erdem werden die Knoten A, B, C, D, E und F benannt. Als (fast) komplettes Bild erh�lt man die linke Abbildung. In diesem Plan k�nnte man noch weitere Maschen einzeichnen, die jeweils aus mehreren Einzelmaschen bestehen.

Nun werden die Ausgangsgleichungen f�r die Rechnung formuliert:

Aus dem Ohm�schen Gesetzt ergeben sich:

1. U1 = R1 * I1
2. U2 = R2 * I2
3. U34 = R34 * I34
4. U5 = R5 * I5
5. U6 = R6 * I6

Aus der Knotenregel ergeben sich :

Knoten A: I1 = I2 + I8
Knoten B: I8 = I34 + I5
Knoten C: I2 = I7 + Ib
Knoten D: I6 = I34 + I7
Knoten E: I1 = I9 + Ib
Knoten F: I9 = I6 + I5

Aus der Maschenregel ergeben sich :
Masche I: U1 +U2 - Ua - Ub = 0		U1 + U2 = Ua + Ub
Masche II: U2 - U34 = 0	bzw.:	U2 = U3
Masche III: Ub + U6 = 0		Ub = -U6
Masche IV: U5 - U6 - U34 = 0		U5 = U6 + U34

Die tats�chlichen Stromrichtungen ergeben sich aus dem Vorzeichen in den einzelnen Rechenergebnissen:
Ist das Vorzeichen positiv, flie�t der betreffende Strom genau in der angenommenen Richtung
Ist das Vorzeichen negativ, flie�t der Strom entgegen der angenommenen Richtung.

Das sind insgesamt 15 Gleichungen mit den 14 Unbekannten
U1, U2, U34, U5, U6, I1, I2, I34, I5, I6, I7, I8, I9, Ib.
Eine der 15 Gleichungen ist �berfl�ssig. Solange man nicht wei�, welche es ist, muss man alle 15 Gleichungen ber�cksichtigen.

Ziel ist es zun�chst, diese 15 Gleichungen mit 14 Unbekannten Schritt f�r Schritt zu reduzieren, bis noch 1 Gleichung mit 1 Unbekannten �brigbleibt.

Sollte dieses Gleichungssystem allerdings nicht l�sbar sein, weil noch passende Gleichungen fehlen, so kann man weitere Gleichungen aus den nicht ausgenutzten Maschen herleiten.
Au�erdem kann man sich an beliebiger Stelle im Plan einen k�nstlichen Knoten erzeugen, auch wenn er nur eine Zuleitung und eine Ableitung besitzt.

Hier noch einmal die Formeln in Reinform und durchnummeriert: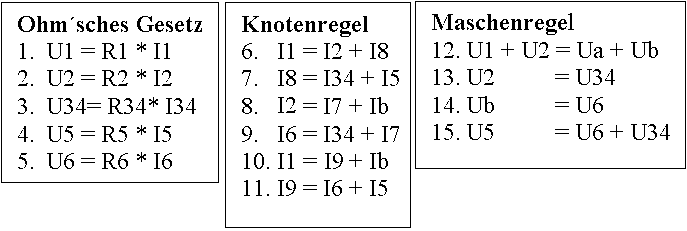
Formel

Da U6 und R6 gegeben sind:

U6 = -Ub = -30V

I6 = U6 / R6 = -30V / 1000Ω = -30mA

Damit sind ab jetzt U6 und I6 bekannt und es bleiben folgende 13 Gleichungen �brig mit den 12 Unbekannten:
I1, I2, I34, I5, I7, I8, I9, Ib, U1, U2, U34, U5

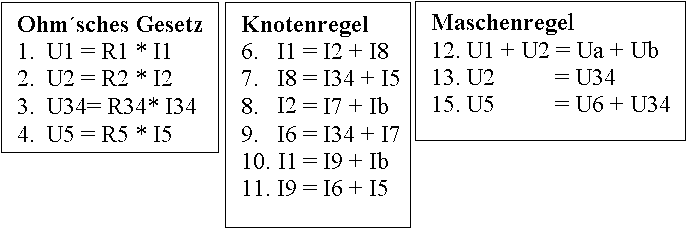Wenn man nun in den Gleichungen(Gl) 12, 13, und 15 die Spannungen ersetzt gem�� den Gl 1...5, erh�lt man das rechts abgebildete Gleichungssystem.

Dies besteht nur noch aus 9 Gl mit den 8 Unbekannnten (Unbek):
I1, I2, I34, I5, I7, I8, I9, Ib,

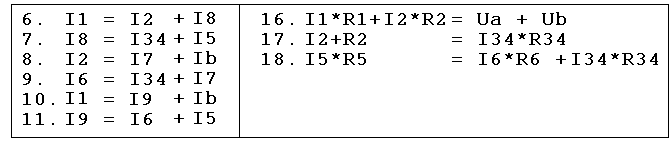Nun wird in allen �brigen Gl I8 ersetzt durch I34 + I5 (Gl.6)

Au�erdem wird in allen �brigen Gleichungen I1 ersetzt durch Ib +I9 (Gl.9)

Die Gl. 6 und 9 werden dann nicht mehr ben�tigt.

Es ergibt sich das Gl.System rechts aus 7 Gl. mit 6 Unbek.
I2, I34, I5, I7, Ib.

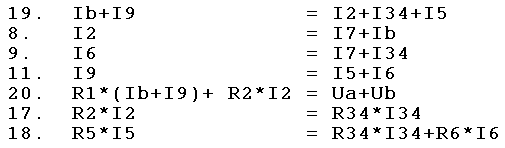Nun wird in allen �brigen Gl. I7 ersetzt durch I6-I34 (Gl.8)

Au�erdem wird in allen �brigen Gleichungen I9 ersetzt durch I5 +I6 (Gl.11)

Die Gl. 6 und 9 werden dann nicht mehr ben�tigt.

Es ergibt sich das Gl.System rechts aus 5 Gl. mit 4 Unbek.
I2, I34, I5, Ib.

Man kann erkennen, dass die Gl. 21 und 22 �quivalent sind (Sie haben die gleiche Information)
Also wird Gl. 21 gestrichen und man erh�lt ein Gleichungssystem aus 4 Gleichungen mit 4 Unbekannten.
I2, I34, I5, Ib.

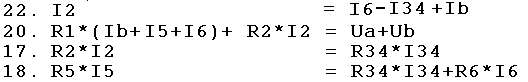I34 wird ersetzt durch I2*R2/R34
und man erh�lt ein Gleichungssystem aus 3 Gleichungen mit 3 Unbekannten.
Das *-Zeichen wird jatzt auch nicht mehr mitgeschrieben (z.B. I2*R2 = I2R2)
3 Gl. mit den 3 Unbek.: I2, I5, Ib.

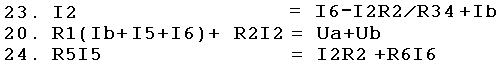Stellt man Gl.23 nach Ib um, so erh�lt man:
Ib = I2*(R34+R2/R34) -I6
Dies wird in Gl. 20 statt Ib eingesetzt.

2 Gl. mit den 2 Unbek.: I2, I5.

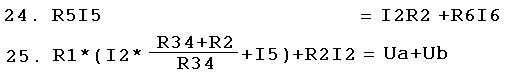Stellt man Gl.25 nach I5 um, so erh�lt man:
I5 = (R2I2+R6I6) / R5
Dies wird in Gl. 24 statt I5 eingesetzt.

1 Gl. mit den 1 Unbek.: I2!!

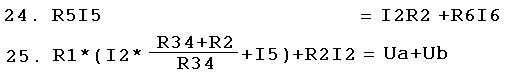Gl.26 muss nun nur noch nach I2 umgestellt werden, und die Gesamtaufgabe ist so gut wie gel�st.

Sp�testens an dieser Stelle sollten Sie sich Gedanken machen, ob denn die Gleichung wenigstens bez�glich der Einheiten stimmen kann!

Hier werden Sie feststellen, dass im Z�hler 3 Spannungen addiert bzw. subtrahiert werden, w�hrend im Nenner 3 Widerst�nde addiert werden.
Spannung / Widerstand ist ein Strom! (Gl�ck gehabt, die L�sungsformel kann stimmen, muss aber nicht!)

Die L�sungsgleichung enth�lt nur noch I2 als Unbekannte, alle anderen Gr��en der Gl. sind bekannt.
Die bekannten Werte werden eingesetzt und I2 kann berechnet werden.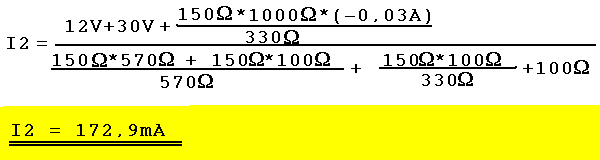

Die restlichen 13 Unbekannten ermittelt man nun, indem man von hier aus r�ckw�rts alle Gleichungen durchsucht, bis man die erste gefunden hat, in der nur noch eine einzige Unbekannte vorkommt.

Sp�testens wenn man an den Ausgangsgleichungen angekommen ist (und nichts �bersehen hat), sind alle Unbekannten berechnet.

Also los

In Gl. 24 kommt als einzige Unbekannte I5 vor.
Gl. 24 nach I5 umstellen, Werte einsetzen und I5 ausrechnen

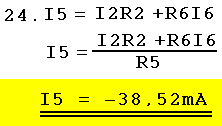Auf analoge Weise ist Gl.20 geeignet, Ib zu berechnen.
Gl. 20 nach Ib umstellen, Werte einsetzen und Ib ausrechnen

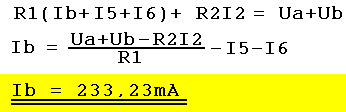In diesem Sinne geht es weiter mit Gl.17, um I34 zuberechnen.
Das weitere Vorgehen ist somit klar und es ergibt sich insgesamt:

Formel

I1=	164,71mA
I2 =	172,9mA
I34=	30,33mA
I3=	I34 = 30,33mA
I4=	I34 = 30,33mA
I5=	-38,52mA
I6=	-30mA
I7=	-60,33mA
I8=	-8,19mA
I9=	-68,52mA
Ia=	I1 = 164,7mA
Ib=	233,23mA
U1=	24,71V
U2=	17,29V
U34=	17,29V
U3=	14,26V
U4=	3,03V
U5=	-12,71V
U6=	-30V

Beachten Sie die Vorzeichen der einzelnen Str�me bzw. Spannungen.
Alle Gr��en, die ein negatives Vorzeichen haben wurden irrt�mlicherweise in der falschen Richtung angenommen.
Die entsprechenden Strom- / Spanungspfeile m�ssen also um 180� gedreht werden.

Trotz der falschen Annahme, f�hrt die Gesamtrechnung zum richtigen Ergebnis!

Zugegeben, diese Art der Berechnung ist sehr schwerf�llig. H�tte man mehr Ahnung von Elektrotechnik, so w�rde man sich den Stromlaufplan vor der Berechnung wesentlich vereinfachen und k�me bei diesem Beispiel schneller zum Ziel.

Andererseits f�hrt diese Methode immer ans Ziel, auch wenn man den Schaltplan nicht vereinfachen kann.

Quickstart

Seite:

Grundlagen der Elektrotechnik

Gleichstromtechnik

Gemischte Schaltungen

Berechnung einer gemischten Schaltung 1

Als Werkzeuge stehen zur Verf�gung:

Nun werden die Ausgangsgleichungen f�r die Rechnung formuliert:

Die tats�chlichen Stromrichtungen ergeben sich aus dem Vorzeichen in den einzelnen Rechenergebnissen:
Ist das Vorzeichen positiv, flie�t der betreffende Strom genau in der angenommenen Richtung
Ist das Vorzeichen negativ, flie�t der Strom entgegen der angenommenen Richtung.

Sp�testens an dieser Stelle sollten Sie sich Gedanken machen, ob denn die Gleichung wenigstens bez�glich der Einheiten stimmen kann!

Die restlichen 13 Unbekannten ermittelt man nun, indem man von hier aus r�ckw�rts alle Gleichungen durchsucht, bis man die erste gefunden hat, in der nur noch eine einzige Unbekannte vorkommt.

Also los

Beachten Sie die Vorzeichen der einzelnen Str�me bzw. Spannungen.
Alle Gr��en, die ein negatives Vorzeichen haben wurden irrt�mlicherweise in der falschen Richtung angenommen.
Die entsprechenden Strom- / Spanungspfeile m�ssen also um 180� gedreht werden.

Zugegeben, diese Art der Berechnung ist sehr schwerf�llig. H�tte man mehr Ahnung von Elektrotechnik, so w�rde man sich den Stromlaufplan vor der Berechnung wesentlich vereinfachen und k�me bei diesem Beispiel schneller zum Ziel.

14

Grundlagen der Elektrotechnik

Gleichstromtechnik

Gemischte Schaltungen

Berechnung einer gemischten Schaltung 1

Als Werkzeuge stehen zur Verf�gung:

Nun werden die Ausgangsgleichungen f�r die Rechnung formuliert:

Die tats�chlichen Stromrichtungen ergeben sich aus dem Vorzeichen in den einzelnen Rechenergebnissen: Ist das Vorzeichen positiv, flie�t der betreffende Strom genau in der angenommenen Richtung Ist das Vorzeichen negativ, flie�t der Strom entgegen der angenommenen Richtung.

Sp�testens an dieser Stelle sollten Sie sich Gedanken machen, ob denn die Gleichung wenigstens bez�glich der Einheiten stimmen kann!

Die restlichen 13 Unbekannten ermittelt man nun, indem man von hier aus r�ckw�rts alle Gleichungen durchsucht, bis man die erste gefunden hat, in der nur noch eine einzige Unbekannte vorkommt.

Also los

Beachten Sie die Vorzeichen der einzelnen Str�me bzw. Spannungen. Alle Gr��en, die ein negatives Vorzeichen haben wurden irrt�mlicherweise in der falschen Richtung angenommen. Die entsprechenden Strom- / Spanungspfeile m�ssen also um 180� gedreht werden.

Zugegeben, diese Art der Berechnung ist sehr schwerf�llig. H�tte man mehr Ahnung von Elektrotechnik, so w�rde man sich den Stromlaufplan vor der Berechnung wesentlich vereinfachen und k�me bei diesem Beispiel schneller zum Ziel.

14

Die tats�chlichen Stromrichtungen ergeben sich aus dem Vorzeichen in den einzelnen Rechenergebnissen:
Ist das Vorzeichen positiv, flie�t der betreffende Strom genau in der angenommenen Richtung
Ist das Vorzeichen negativ, flie�t der Strom entgegen der angenommenen Richtung.

Beachten Sie die Vorzeichen der einzelnen Str�me bzw. Spannungen.
Alle Gr��en, die ein negatives Vorzeichen haben wurden irrt�mlicherweise in der falschen Richtung angenommen.
Die entsprechenden Strom- / Spanungspfeile m�ssen also um 180� gedreht werden.