
Musterlösungen, Übersicht und Links
Musterlösungen

Berufskolleg Mitte - Essen


|
Autoelektrik ( Startseite) Musterlösungen, Übersicht und LinksMusterlösungen |
 Berufskolleg Mitte - Essen |

|
| vorige Seite | 4.01 Anwendungen der Integralrechnung4.01.01 Gesamteinkommen im Erwerbsleben |
nächste Seite |
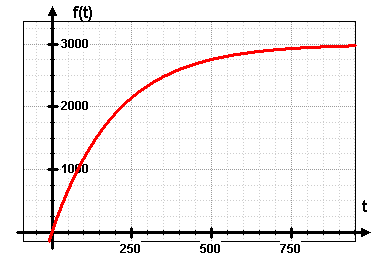
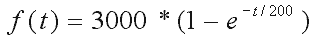
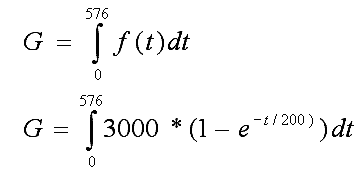
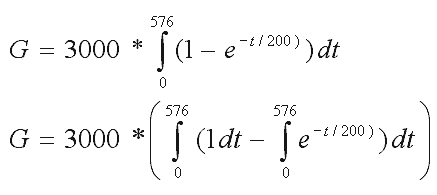
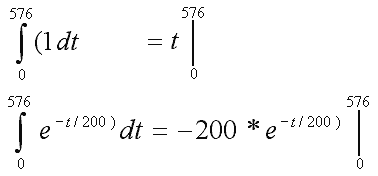
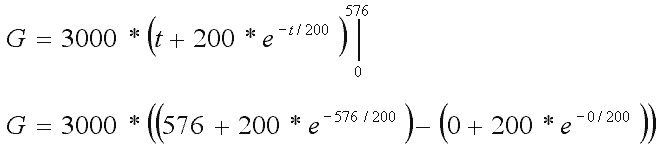
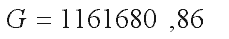 Das Ergebnis
Das Ergebnis |
vorige Seite nächste Seite |
 email an Autor |
Musterlösungen, Übersicht und Links |
 Autoelektrik Startseite |
 Berufskolleg Mitte - Essen |