Seitenende

Autoelektrik Startseite

Grundlagen der Elektrotechnik

Spule im Gleichstromkreis

xxxxxx


yyyyyy


zzzzzz
















Seitenanfang

xxxxxx

yyyyyy















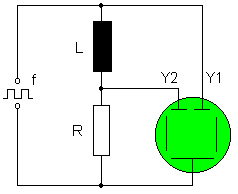Spulenstroms Ein-/Ausschalten Mit der nebenstehenden Schaltung kann man sehr gut beobachten, wie sich der Strom durch die Spule verhält, wenn man die Spannung einschaltet bzw. ausschaltet:
Die Schaltung besteht aus den Elementen:
  1. Frequenzgenerator als Spannungsquelle
  2. Spule, deren Ein- Ausschaltverhalten untersucht werden soll
  3. Messwiderstand
  4. Zweikanaloszilloskop als Messgerät




Frequenzgenerator mit Link zu Conrad Electronic Ein Frequenzgenerator ist ein Gerät, das an einem Ausgang ein Signal erzeugt, welches man für Messungen gebrauchen kann. Die Signalspannung ist ebenso wie der Signalstrom nur in engen Grenzen variabel. Dafür kann die Frequenz von etwa 1Hz bis 1MHz verstellt werden. Außerdem können die Signalformen Sinus, Dreieck und Rechteck eingestellt werden.


Für den Versuch zur Beobachtung des Ein- und Ausschaltstroms einer Spule wird der Generator auf Rechtecksignal gestellt. Damit hat man einen Sklaven, der die Spannung regelmäßig ein- u. ausschaltet und muss es nicht selber tun.







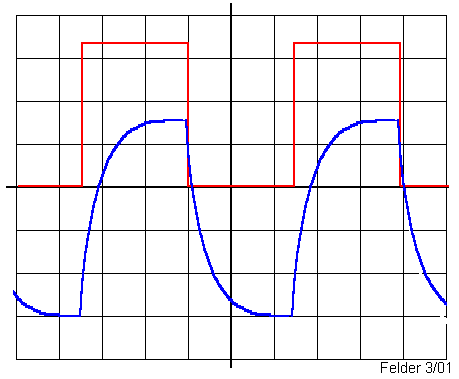Oszilloskpbild von Spulenspannung und Spulenstrom Bei dem Versuch könnte auf dem Bildschirm des Oszilloskops ein solches Bild entstehen. Dabei bedeutet z.B. eine horizontale Gittereinheit 1ms, eine vertikale Gittereinheit 1V (für die rote Linie) und 0,1V (für die blaue Linie). Die rote Rechteckspannung zeigt das Ausgangssignal der Spannungsquelle (=Eingangssignal der Schaltung). Der blaue Kurvenzug zeigt den zeitlichen Verlauf der Spannung am Widerstand R. Da der Wert des Widerstands bekannt ist (z.B. 100 Ω), lässt sich somit der Strom durch den Widerstand für jeden auf dem Scope angezeigten Zeitpunk nach dem Ohmschen Gesetz berechnen.Insbesondere ergibt sich, dass der Strom proportional zu der Spannung ist. Also beschreibt der blauen Kurvenzug ebensogut als Stromverlauf durch den Widerstand wie dessen zeitlichen Spannungsverlauf.
Nach den Gesetzen der Reihenschaltung ist der Strom durch die Spule zu jedem Zeitpunkt genau so groß wie der Strom durch den Widerstand. Damit entspricht die blaue Linie also auch dem zeitlichen Stromverlauf durch die Spule.
Der Trick mit dem Reihenwiderstand ermöglicht es auf diese Weise einen Strom indirekt zu messen, obwohl das Scope direkt nur Spanungen messen kann.



Schaltet man an einer Spule die Spannung ein, so steigt die Stromstärke von 0A zunächst rasch an. Je größer die Stromstärke durch die Spule bereits ist, desto langsamer wird der weitere Stromanstieg, bis schließlich der Sättigungsstrom erreicht ist und die Stromstärke konstant bleibt.



Mit den bekannten Werten der Schaltung und des Scopebildes sowie einigen Formeln kann man nun die Induktivität der Spule berechnen.

bekannte Größen:

Rechteckspannung des Funktionsgenerators 0V und 3,4V einstellbar am Funktionsgenerator
Periodendauer der Rechteckspannung 4,9 ms einstellbar am Funktionsgenerator
Wert des Messwiderstands 100 Ωablesbar auf dem Widerstand

Damit lässt sich berechnen:

Widerstand der Spule: In der Reihenschaltung muß die Summe der Einzelspannungen gleich der Gesamtspannung sein.

Also gilt z.B. für den Sättigungsfall:

Gesamtspannung am Frequenzgenerator = 3,4V
Spannung am Widerstand = 0,45V		 USpule = UGenerator - UWiderstand = 3,4V - 0,45V = 2.95V
In der Reihenschaltung ist das Widerstandsverhältnis genau so groß wie das Spannungsverhältnis.
Da die Spannung an der Spule 6,55 mal so groß ist wie die am Widerstand (2,95V = 6,55 * 0,45V), muss auch der Spulenwiderstand 6,55 mal so groß sein, wie der Messwiderstand.
RSpule= 6,55 * RWiderstand= 6,55 * 100 Ω.= 655 Ω
Frequenz des Rechtecksignalsf = 1 / T
Periodendauer T am Scope ablesbar		f= 1/ 4,9ms = 204 Hz

Aus der Dauer bis zum Erreichen des Sättigungsstroms kann man die Zeitkonstante für diese Widerstands-Spulen-Schaltung bestimmen:

Zeitkonstante t tSättigung » 5 * t (Faustformel für Praktiker) t » tSättigung / 5 = 2ms / 5 = 0,4ms
Induktivität L t = L / R

L Induktivität der Spule
R Gesamtwiderstand der Schaltung, also RWiderstand + RSpule		 t * Rges = 0,4ms * 755 Ω = 304ms Ω = 304 mH

1 H = 1 Henry = 1 Vs / A (Einheit der Induktivität)















































Ohne den Messwiderstand in der oben genutzten Schaltung hätte man kein Oszilloskopbild erhalten. Dieser Messwiderstand ist bei der normalen Nutzung von Spulen natürlich nicht erforderlich, im Gegenteil würde er eher stören, da er den Spulenstrom unnötig reduziert. Wenn es also keinen zusätzlichen Widerstand im Spulenstromkreis gibt, so bleibt doch der Ohm´sche Widerstand der Spule, der in die Berechnung der Zeitkonstanten einzubeziehen ist.


Damit Sie sich unter der Größe 1H etwas mehr vorstellen können, sei folgendes angemerkt:

Ändert sich der Strom durch eine Spule mit der Induktivität 1H genau um 1A/s, so wird in der Spule eine Spannung von genau 1V induziert.










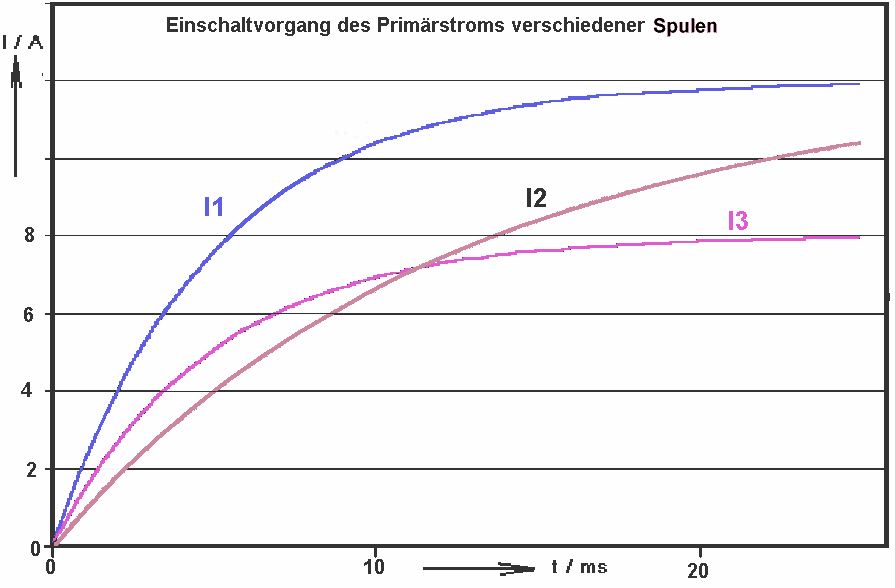Spulenströme bei unterschiedlichen Spulen Dieses Diagramm entstand bei der Messung von drei verschiedenen Spulen.

Nehmen wir an, dass alle Spulen an der Bordnetzspannung von 12V angeschlossen waren. Dann muss der Widerstand der Spule 1 1 Ω betragen haben, der Widerstand der Spule 3 jedoch 1,5 Ω. Diese Werte sind aus den Sättigungsströmen jeweils zu berechnen. Den Sättigungsstrom der Spule 2 kann man nur erahnen: er könnte auch bei 12A liegen wie der Sättigungsstrom der Spule 1. Damit hätte die Spule 2 denselben Widerstand wie Spule 1.

Bei Spule1 und Spule3 fällt auf, dass beide dieselbe Zeit benötigen, um den Sättigungswert zu ereichen, Spule 2 benötigt jedoch viel länger als die beiden anderen Spulen. Daraus folgt, dass die Zeitkonstanten der Spule1 und 3 gleich groß sind, die Zeitkonstante von Spule 2 jedoch größer. Auf diese Weise kann man die Spuleneigenschaften miteinander vergleichen. Sie können nun auch Rückschlüsse über die Induktivitäten der Spulen ziehen.

Als Bestimmungsgrößen für Spulen gibt es nur die beiden folgenden:
  1. den Ohmschen Widerstand der Spule R
  2. die Induktivität der Spule L
Der Widerstand der Spule lässt sich direkt aus dem Leiterwiderstand berechnen.

Die Induktivität dagegen hängt ab von:
  1. Windungszahl N
  2. Spulenlänge l
  3. Spulenquerschnitt A
  4. Material des Spulenkerns mr
  5. magnetische Feldkonstante oder Permeabilitätskonstante m 0 ( = 1,256 * 10-6 H/m)
nach folgender Formel:

L = m0 * mr * N2 * A / l




Während die magnetische Feldkonstante m0 universell gilt und konstant ist, ist die relative Permeabilität sowohl materialabhängig und bei Magnetwerkstoffen (Eisen, Kobalt, Nickel, bestimmte Legierungen mit diesen Materialien)) auch noch von der magnetischen Feldstärke. Bei den nichtmagnetischen Werkstoffen ist diese Zahl etwa 1. Man unterscheidet die
diamagnetischen Werkstoffe mit mr <1 von den
paramagnetischen Werkstoffe mit mr >1.
Bei den ferromagnetischen Werkstoffen ist mr wesentlich größer als1, hängt aber, wie oben schon erwähnt von der Feldstärke ab. Diese Werte variieren zwischen 1000 und mehreren 10000, die man von Fall zu Fall in Kennlinien bzw. Tabellen nachschauen muß.

Ein Eisenkern in einer Kupferspule kann also deren Induktivität um den Faktor 5000 erhöhen!





















xxxxxx

yyyyyy

zzzzzz















yyyyyy

zzzzzz

Seitenende















Einsatz von Spulen im Kfz:

  1. Relais
  2. Magnetschalter des Starters
  3. Zündspule
  4. Funkentstörung
  5. Magnetventile
  6. Wicklungen in Motoren
  7. Erregerwicklung des Generators
  8. Ständerwicklung des Generators
  9. Spulen in Induktivgebern














Seitenanfang Quickstart eMail an Autor Startseite zurückblättern vorblättern Stichwortverzeichnis Aufgaben Seite:

30