Automobilelektrik
Grundlagen der Elektrotechnik
Gleichstromtechnik
Leiterwiderstand
|
spezifischer Widerstand - Formeln |
|
|
Die unterschiedlichen Materialen leiten den Strom verschieden gut. Je nach Leitfähigkeit teilt man die Werkstoffe in Leiter, Halbleiter und Nichtleiter (Isolatoren) auf. Um die Werte der Materialien sinnvoll miteinander vergleichen zu können, notiert man den Widerstand von Proben gleicher Abmessungen (1m lang 1mm2 Querschnittsfläche) aus unterschiedlichen Stoffen. Diesen Wert nennt man Spezifischer elektrischer Widerstand eines Materials. Das Formelzeichen ist r (rho), und es gilt: | ||
r = R * A / l | bzw. | R = r*l/A |
|
mit : r spezifischer elektrischer Widerstand A Querschnittsfläche des Materials l Länge des Materials | ||
|
Je geringer der spezifische Widerstand
desto besser leitet das Material. Beachten Sie in der untenstehenden Tabelle die gewaltige Spreizung zwischen den guten Leitern und den guten Isolatoren. | ||
|
Mit den oben gegebenen Formeln lässt sich also der Widerstand eines Drahtes berechnen, wenn man seinen Querschnitt, seine Länge
und den spez. Widerstandswert des in Frage kommenden Materials kennt. Die Einheit von r ist Ohm *qmm / m ( 1Ohm *qmm / m = 10 -6 Ohm * m) Der Kehrwert vom spezifischen elektrischen Widerstand ist der spezifische elektrische Leitwert | ||
|
spezifischer Widerstand - Tabelle |
|
| Nr | Material | Spezifischer Widerstand Wmm2/m |
| 1 | Aluminium | 0,028 |
| 3 | Blei | 0,21 |
| 4 | Eisen | 0,098 |
| 5 | Gold | 0,022 |
| 6 | Kohle | 50 ... 100 |
| 7 | Kupfer | 0,0178 |
| 8 | Nickel | 0,07 |
| 9 | Platin | 0,105 |
| 10 | Quecksilber | 0,96 |
| 11 | Silber | 0,016 |
| 13 | Wolfram | 0,055 |
| 14 | Zink | 0,059 |
| 13 | Bürstenkohle | 40 ... 100 |
| 14 | 10% Schwefelsäure | 1000000 |
| 15 | Glas | 1017 ...1018 |
| 16 | Papier | 1021 ...1022 |
| 17 | Seewasser | 300000 |
| 18 | dest. Wasser | 1010 |
| 13 | Silizium | 1011 |
|
Temperaturkoeffizient - Formeln |
|
|
Bei erhöhter Temperatur leiten die Metalle schlechter als in kaltem Zustand. Die Ursache liegt in den stärkeren Atomschwingungungen begründet. Dadurch können sich die Elektronen im Gitter nicht mehr so frei bewegen wie bei relativ ruhigen Atomen (kalt). Dieses Phänomen beschreibt man durch den sogenannten Temperaturkoeffizienten alpha. Alpha gibt an, um wieviel sich der Widerstand eines bestimmten Materials relativ ändert, wenn sich die Temperatur um 1 °C erhöht. Die Einheit von alpha ist 1/K | ||
R1 = R0 *( 1+alpha* deltaT) | bzw. | deltaR = R0 *alpha * deltaT |
|
mit : R1 Widerstand bei hoher Temperatur R0 Widerstand kalt alpha Temperaturkoeffizient deltaT Temperaturdifferenz (=T1 - T0) deltaR Widerstansdifferenz (= R1 - R0) | ||
|
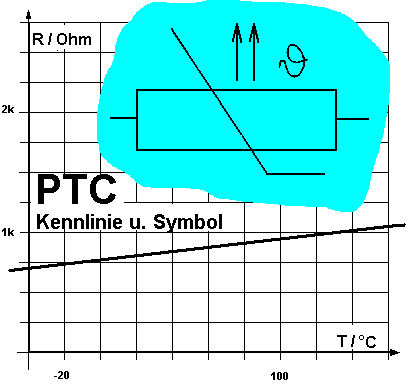
Diese Formeln gelten mit hinreichender Genauigkeit nur in kleinen Temperaturbereichen (ca zwischen -20°C und 150 °C). Je kleiner alpha, desto weniger ändert sich der Widerstand mit der Temperatur. Alle Materialien die einen Positiven Temperatur Coeffizienten haben, nennt man PTC. Das sind im wesentlichen alle Metalle. Diese erhöhen ihren Widerstand bei Erwärmung. Im Gegensatz dazu kennt man auch NTC-Widerstände, die bei Erwärmung ihren Widerstand verringern. | ||
|
Temperaturkoeffizient - Tabelle |
|
| Nr | Material | alpha/ 1/K |
Tabelle der Temperaturkoeffizienten der Widerstände verschiedener Materialien (20°C). | ||
| 1 | Aluminium | 0,0043 |
| 2 | Blei | 0,004 |
| 3 | Eisen | 0,0056 |
| 4 | Gold | 0,0039 |
| 5 | Iridium | 0,0041 |
| 6 | Kalium | 0,005 |
| 7 | Kobalt | 0,0066 |
| 8 | Kupfer | 0,0039 |
| 9 | Magnesium | 0,004 |
| 10 | Molybdän | 0,0047 |
| 11 | Natrium | 0,0055 |
| 12 | Nickel | 0,0062 |
| 13 | Platin | 0,0038 |
| 14 | Quecksilber | 0,00092 |
| 15 | Silber | 0,0038 |
| 16 | Wolfram | 0,0041 |
| 17 | Zink | 0,0037 |
| 18 | Zinn | 0,0046 |
| 19 | Konstantan | 0,00003 |
| 20 | Manganin | 0,00002 |
|
PTC im Kfz |
|
 |
Da der Widerstand von PTCs von der Temperatur abhängt, eignen sie sich prinzipell ebenso wie NTCs zur
Temperaturmessung . Da bei NTCs die Kennlinie jedoch steiler verläuft als bei PTCs, reagieren NTCs empfindlicher auf Temperaturänderungen und messen daher genauer. Andererseits lassen sich NTCs nicht bei hohen Temperaturen einsetzen. In diesen Fällen werden sogenannte Hochtemperatur Platin Temperaturfühler eingesetzt. Die Eigenschaft von PTCs, bei kalten Temperaturen besser zu leiten als bei warmen, gibt ihnen auch den Namen Kaltleiter. PTCs nutzt man im Kfz als sich selbst regelnde Heizelemente z.B. bei der Lambdasondenheizung oder bei Glühstiftkerzen für Dieselmotoren. Da sie kalt einen niedrigen Widerstand haben, fließt dann ein entsprechend hoher Strom. Dadurch hat man eine gewünschte hohe Heizleistung und das zu erwärmende Element kommt schnell auf Betriebstemperatur. Je heisser der PTC jedoch wird, desto grösser wird sein Widerstand und als Folge davon wird der Strom durch ihn umso kleiner. Damit sinkt entsprechend auch die Heizleistung. Solche Elemente benötigen zur Temperaturregelung kein Steuergerät. Mit geringstem Aufwand erzielt man den gewünschten Effekt. Auch wenn die Lambdasonde durch das heisse Abgas erhitzt ist, hat das PTC Heizelement seinen hohen Widerstand und zieht keinen nennenswerten Strom mehr. |
 |
Quickstart |  |
 |
 |
 |
 |
Seite:9 |