
Musterlösungen, Übersicht und Links
Musterlösungen

Berufskolleg Mitte - Essen


|
Autoelektrik ( Startseite) Musterlösungen, Übersicht und LinksMusterlösungen |
 Berufskolleg Mitte - Essen |

|
| vorige Seite | 2.08 Trigonometrische Funktionen |
nächste Seite |
1. Aufgabe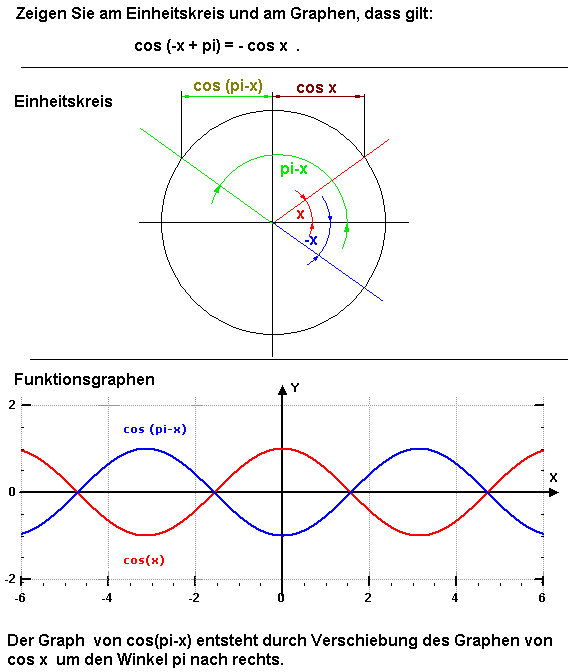 |
2. Aufgabe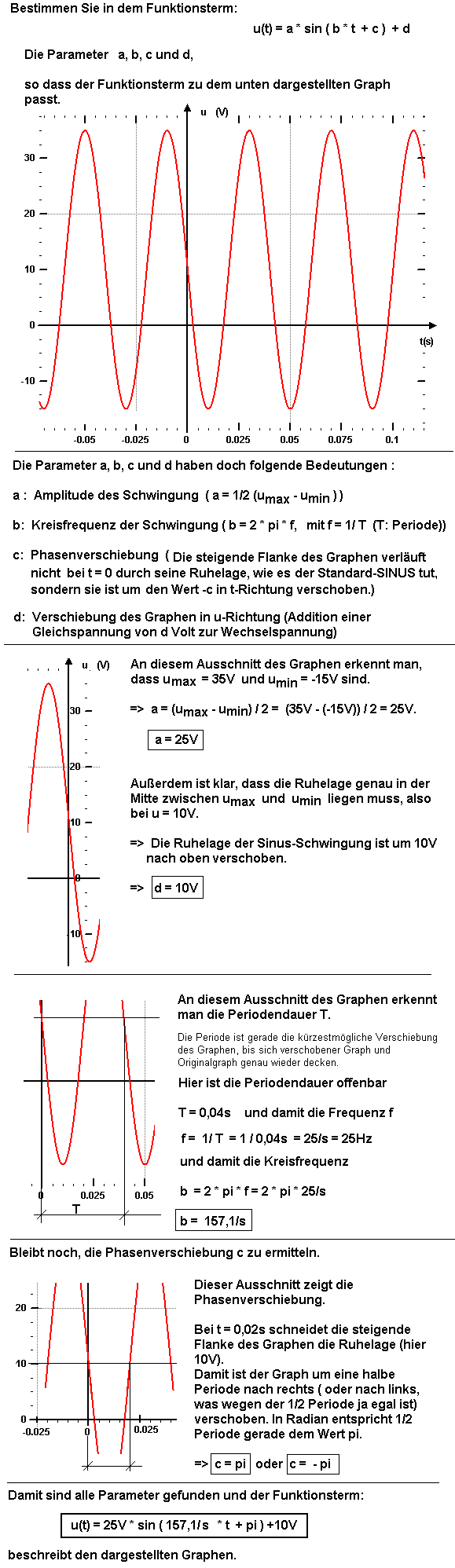 |
3. Aufgabe |
4. Aufgabe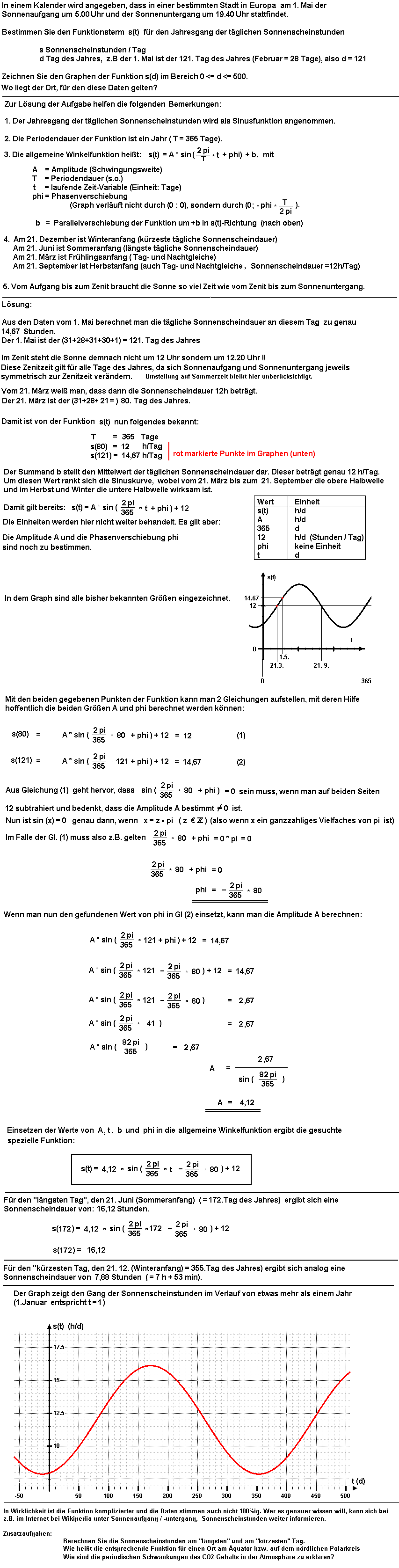 |
5. Aufgabe
Gegeben ist ein 3,8L, 4-Zylinder-4-Takt-Reihenmotor.
Der Hub beträgt 120mm, die Pleuelstange ist 150mm lang und die Kompressionshöhe ist 25mm.
Die Drehzahl beträgt gerade 3000/min.
Aufgaben:
1. Geben Sie eine übliche Zündfolge an.
2. Wie lauten für diese Zündfolge die Funktionen f1(t) ...f4(t) für die Zylinder 1...8 , die den zeitlichen Verlauf des Abstands des jeweiligen Kolbenbodens von der Kurbelwellenachse beschreiben?
Nehmen Sie dazu an, die Kolben bewegen sich sinusförmig auf und ab.
3. Zeichnen Sie die Funktionsgraphen.
__________________________________________________________________________________________
Lösung:
1.
Eine übliche Zündfolge des 4-Zyl-4-Takt-Reihenmotors ist 1342.
Daraus folgt:
1. der 1. und der 4. Kolben bewegen sich synchron zueinander
2. der 2. und der 3. Kolben bewegen sich synchron zueinander
3. der 1. Kolben macht eine gegensinnige Bewegung wie der 2.
bzw. Kolben 1/4 bewegen sich um 180° (pi) phasenversetzt
wie Kolben 2/3
---------------------------------------------------------------------
Es sei:
y1(t): Abstand Kolbenboden 1.Zyl. - Kurbelwellenachse als Funktion der Zeit
Dieser Abstand ändert sich ständig und periodisch mit der KW-Drehung.
Die allgemeine Form einer Sinusfunktion lautet:
y1(t) = A * sin(2*pi*f*t +C) + D
mit den zu bestimmden Größen:
A: Amplitude
f: Frequenz
C: Phasenverschiebung
D: Offset (Verschiebung der Ruhelage in y-Richtung).
----------------------------------------------------------
mit den gegebenen Abmessungen des Motors ergibt sich:
Kolben 1 in OT: => ymax= 60 + 150 + 25 = 235 (mm)
Kolben 1 in UT: => ymin= -60 + 150 + 25 = 115 (mm)
Der Kolben bewegt sich um den Offset D=(235+115)/2 = 175.
Der Kolben bewegt sich mit der Amplitude A=(235-115)/2 = 60 nach oben/ unten.
=> y1(t) = 60*sin(2*pi*f*t +C) + 175
Die Zeitachse soll sinnvollerweise die Einheit s haben
bei 3000/min ist f = 50Hz
=> y1(t) = 60*sin(2pi*50*t + C) + 175
Der Wert C ist für einen Zylinder frei wählbar, weil es in dieser Aufgabe keinen
speziellen Startzeitpunkt und keine spezielle Startposition der Kurbelwelle gibt.
Hat man sich jedoch für einen Zylinder festgelegt, so ist C für jeden der übrigen
3 Kolben dieses Motors nicht mehr frei wählbar, sondern hängt jeweils von der
Zündfolge ab.
Mit der oben angegebenen Zündfolge ergibt sich:
y1(t) = y4(t) = 60*sin(100pi * t) + 175
y2(t) = y3(t) = 60*sin(100pi * t + pi) + 175
---------------------------------------------
|
6. Aufgabe |
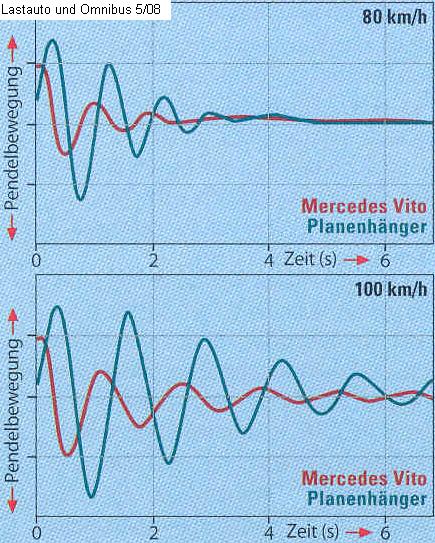 Durch kurzes Anreißen des Lenkrades hat man das Gespann bei zwei verschiedenen Geschwindigkeiten ins Schlingern gebracht, wie es auch durch
plötzlichen Seitenwind auftreten könnte.
Durch kurzes Anreißen des Lenkrades hat man das Gespann bei zwei verschiedenen Geschwindigkeiten ins Schlingern gebracht, wie es auch durch
plötzlichen Seitenwind auftreten könnte.
| www.kszofingen.ch | interaktive Mathetests | www.mathe-online.at | www.ies.co.jp | engl. Mathe-Java-Applets | mathenexus.zum.de | www.arndt-bruenner.de | mathematik.zum.de | www.tutorvista.com | kostenpflichtige Nachhilfe weltweit jederzeit |
 |
vorige Seite nächste Seite |
 email an Autor |
Musterlösungen, Übersicht und Links |
 Autoelektrik Startseite |
 Berufskolleg Mitte - Essen |