	Autoelektrik ( Startseite) Musterlösungen, Übersicht und Links Musterlösungen	Berufskolleg Mitte - Essen
vorige Seite	2.07 Klassenarbeit zu Exp.- u. Log.-Funktionen	nächste Seite

1. Aufgabe

2. Aufgabe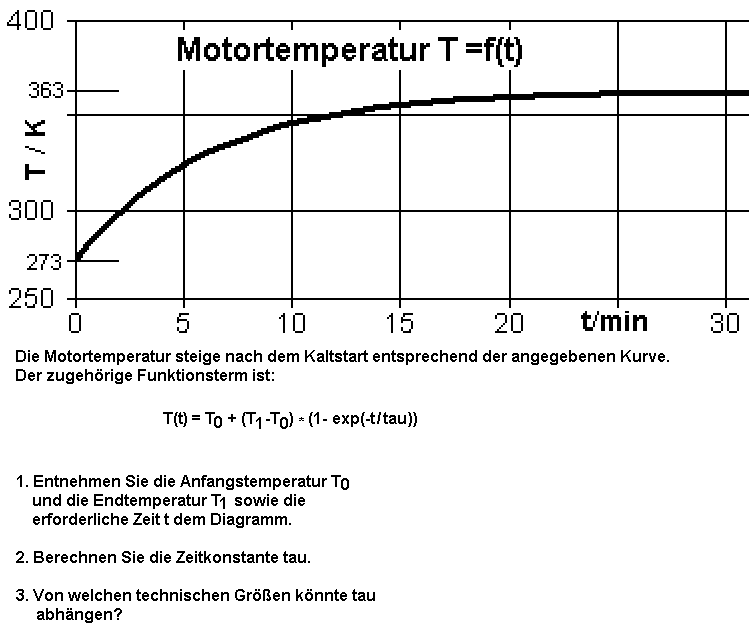

3. Aufgabe

4. Aufgabe

5. Aufgabe

6. Aufgabe

7. Aufgabe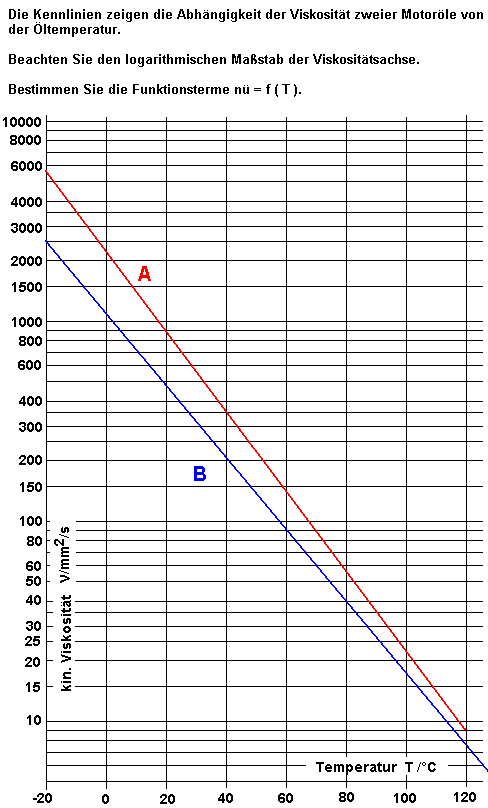

8. Aufgabe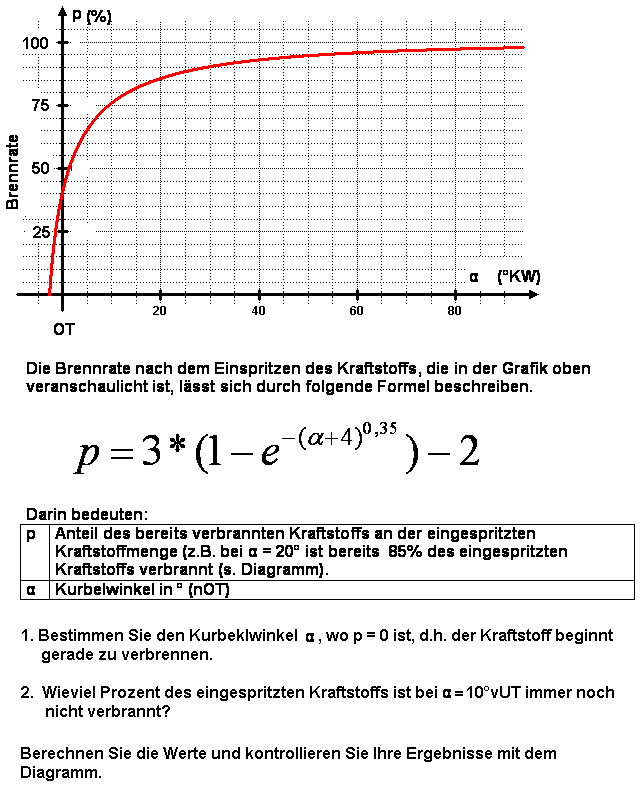

9. Aufgabe

10. Aufgabe

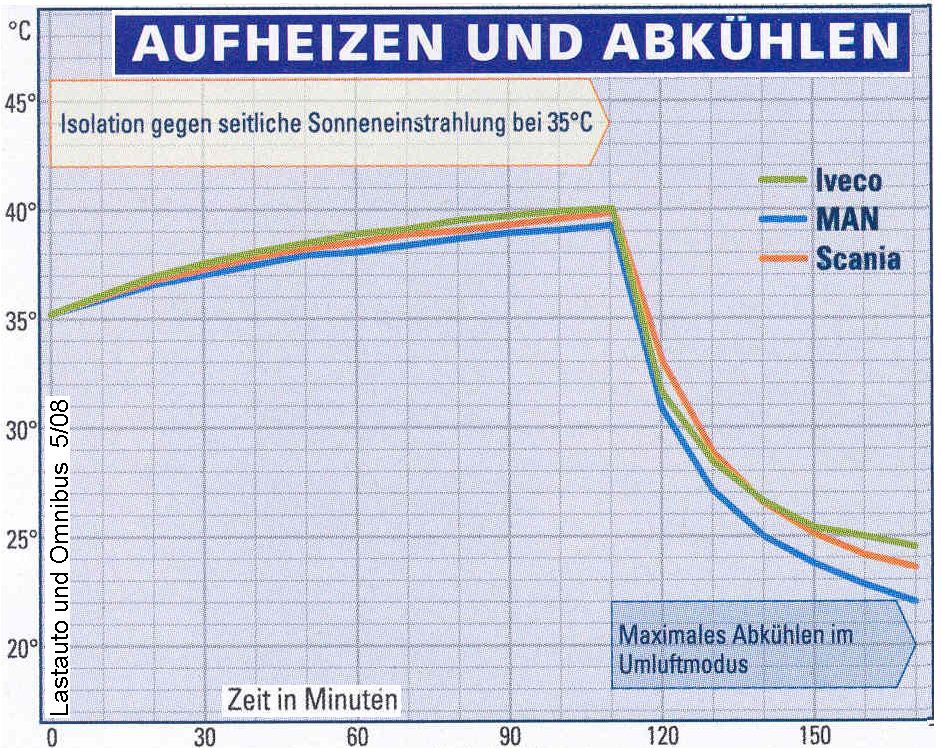
Aufheiz- / Abkühlkurven von Fahrerkabinen

In einer Klimakammer wurden die Klimaanlagen verschiedener Fahrzeuge getestet.

Die Fahrzeuge standen zunächst bei einer "Außentemperatur" von 35°C im "Schatten" und heizten sich auf.

Anschließend wurde die Kabine seitlich bestrahlt, wie es auch die Sonne hätte tun können.

Nach 110 Minuten wurden dann die Klimaanlagender Fahrzeuge aktiviert.

Dabei entstanden die dargestellten Aufheiz- und Abkühlkurven.

Aufgabe: Wählen Sie ein Fahrzeug und bestimmen Sie dafür die Terme der zugehörigen Aufheizfunktion und der Abkühlungsfunktion.

11. Aufgabe

In welcher Reihenfolge müssen die einzelnen Grundoperationen:
* Strecken / Stauchen in x- oder y-Richtung,
* Spiegeln an x- oder y-Achse,
* Verschieben in x- oder y-Richtung,
* Rotation

ausgeführt werden, um aus der Grundgleichung

y₁ = e^x

y₂ = 5 * (1 - e^(-0,5x))

12. Aufgabe

Eine 1mm dicke Glasscheibe einer bestimmten Glassorte arbosbiert 1% des auftreffenden Lichts.
Welcher Anteil des Lichts, das eine 100mm dicke Linse aus diesem Glas durchdringt, bleibt hinter der Linse noch übrig?

Hinweis 1: Wenn Licht ein Medium durchdringt, so wird der absorbierte Teil der Lichtenergie in Wärme umgewandelt.
Hinweis 2: Diese Falle ist doch wohl etwas zu wenig getarnt, als dass da jemand hineinstolpern würde, oder?

13. Aufgabe

Gesucht wird eine Funktion f(x), die sich bei großen x-Werten (z.B. x > 3) annähernd so verhält wie die Funktion
f1(x) = 5x^2+ 10
und für kleine x-Werte (z.B. x < -3) annähernd so verhält wie die Funktion
f2(x) = e^(-3x)

Zeichnen Sie verschiedenfarbig in ein gemeinsames Koordinatensystem (-5 < x < 5) die Graphen der Funktionen f1 und f2.
Bezeichnen Sie diese Graphen.
Ermitteln Sie einen geeigneten Funktionsterm für die gesuchte Funktion f und tragen Sie deren Graph auch in das Koordiantensystem ein.

Begründen Sie in möglichst wenigen aussagefähigen Sätzen, warum sich Ihre Funktion f(x) so verhalten muss wie gefordert.

14. Aufgabe

Für welche Werte von x (mindestens 4-stellige Genauigkeit) stimmen folgende Gleichungen:

a) 5 * e^(-x²) = 2

b) 5x⁴ * e^(-x²) = 2

15. Aufgabe

Es wird behauptet, dass 2 Exponentialfunktionen, die völlig unterschiedliche Basiswerte nutzen, trotzdem völlig gleiche Funktionsgrafen erzeugen können.
Sie sollen diese Behauptung zwar nicht allgemein beweisen, aber weisen Sie dies für folgendes Beispiel nach:

a) f₁(x) = 5 * e^-3(x+5)

b) f₂(x) = a * 10^b(x+5)

Kurz und gut: Bestimmen Sie a und b, so dass die Grafen der beiden Funktionen deckungsgleich sind.

16. Aufgabe

Firma Duroplast schaffte sich am 1.1.2005 eine neu Spritzgussmaschine für 86500 Euro an.
Der Wert dieser Maschine wird degressiv mit 10% pro Jahr abgeschrieben.
Das bedeutet, dass am Ende eines beliebigen Jahreszeitraums der Buchwert dieser Maschine 10% kleiner ist als zu Beginn dieses Jahreszeitraums.

Mit welchem genauen Wert stand die Maschine am 31.12. 2011 in der Firmenbilanz? (ca 46000)
Wie heißt der Funktionsterm, der diese spezielle Abschreibung darstellt?
An welchem Tag hatte die Maschine einen Buchwert von genau 50000 Euro? (an irgendeinem Februartag)
Zeichnen Sie den Graphen für die ersten 20 Abschreibungsjahre.

17. Aufgabe

Von einem NTC-Widerstand ist der Funktionsterm bekannt:

R(T) = R1 + R0 * e^(T/T0)

Außerdem weiß man, dass R1 = 250Ω und T0 = 200K betragen und dass der Widerstand bei 350K genau 350Ω beträgt.

1. Bestimmen Sie die konkrete Funktionsgleichung.
2. Berechnen Sie die Widerstände bei T1= 253K und T2 = 353K.
3. Wie groß ist die Temperatur, wenn der Widerstand 1kΩ beträgt?
4. Zeichnen Sie den Graphen im Bereich T = 200K … 400K

18. Aufgabe

Kochrezept

1. f₁(x) = e^x
2. f₂(x) entsteht aus f₁(x) durch Spiegelung an der x-Achse.
3. f₃(x) entsteht aus f₂(x) durch Streckung in y-Richtung um den Faktor 100.
4. f₄(x) entsteht aus f₃(x) durch Spiegelung an der y-Achse.
5. f₅(x) entsteht aus f₄(x) durch Streckung in x-Richtung um den Faktor 5.
6. f₆(x) entsteht aus f₅(x) durch Verschiebung in um den Wert 20 Einheiten nach unten.
7. f₇(x) entsteht aus f₆(x) durch Verschiebung in x-Richtung um 50 Einheiten nach rechts.
_______________________
Wie heißt der Funktionsterm von f₇(x)?
Skizzieren Sie alle 7 Graphen und tragen Sie in jede Skizze jeweils die Koordinaten eines typischen Punkts des Graphen ein.
Es muss erkennbar sein, welcher Graph zu welcher Funktion gehört!

Rohemissionen NOX und HC

19. Aufgabe

Diesel-Roh-Emissionen

Ermitteln sie Funktionsterme, die die beiden Rohemissionsverläufe von HC und NOx so wiedergeben, wie es etwa dem jeweiligen mittleren Verlauf der beiden Toleranzbänder entspricht.

Hier sind einige Links zu finden, die zu interessanten / hilfreichen Matheseiten im WWW führen.

www.kszofingen.ch	interaktive Mathetests
www.mathe-online.at
www.ies.co.jp	engl. Mathe-Java-Applets
mathenexus.zum.de
www.arndt-bruenner.de
mathematik.zum.de
www.tutorvista.com	kostenpflichtige Nachhilfe weltweit jederzeit

vorige Seite

nächste Seite

Musterlösungen, Übersicht und Links

Autoelektrik Startseite

Berufskolleg Mitte - Essen