	Autoelektrik ( Startseite) Musterlösungen, Übersicht und Links Musterlösungen	Berufskolleg Mitte - Essen
vorige Seite	3.13 Extremwertaufgaben	nächste Seite

1. Aufgabe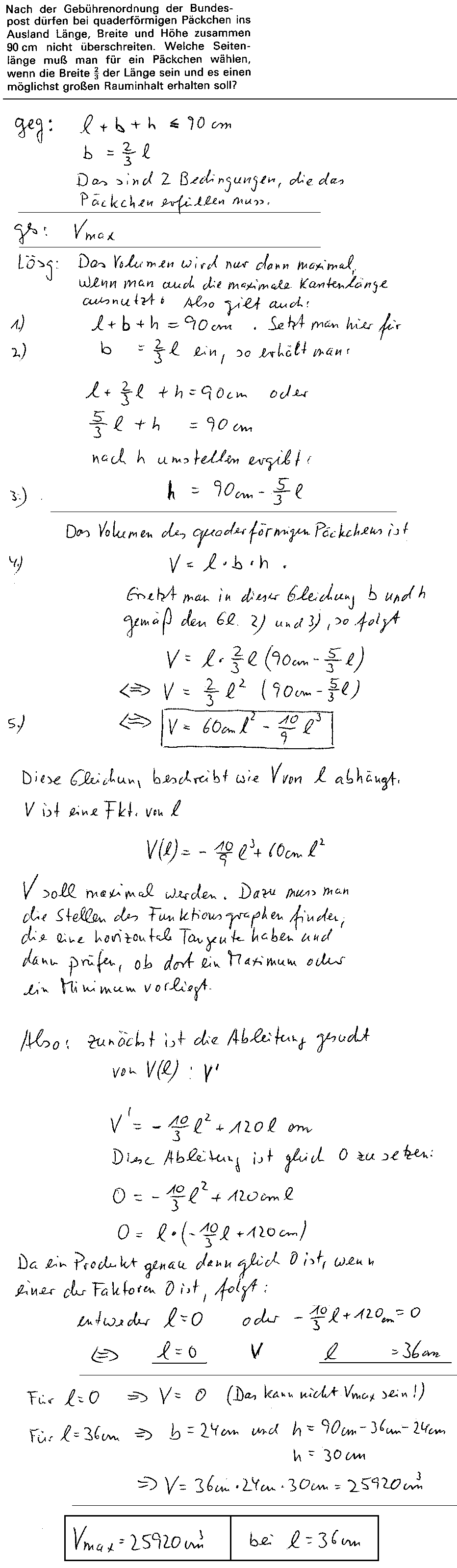

2. Aufgabe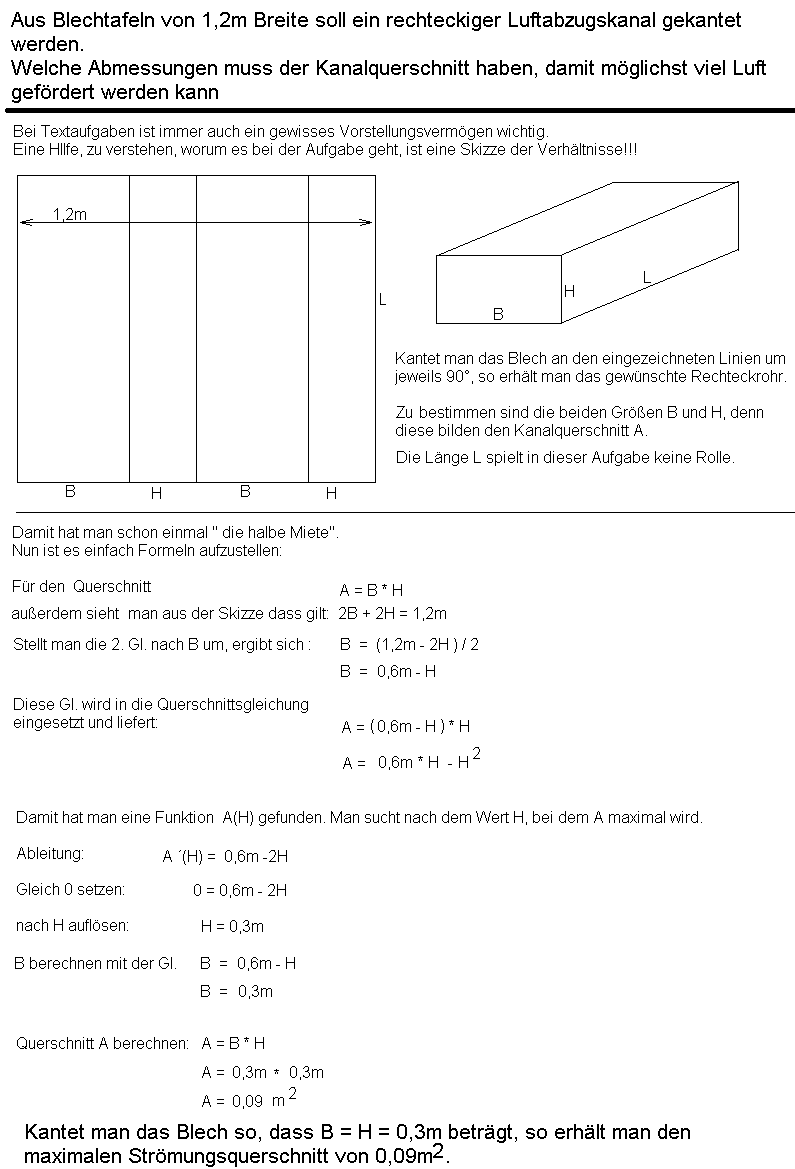

3. Aufgabe

4. Aufgabe

5. Aufgabe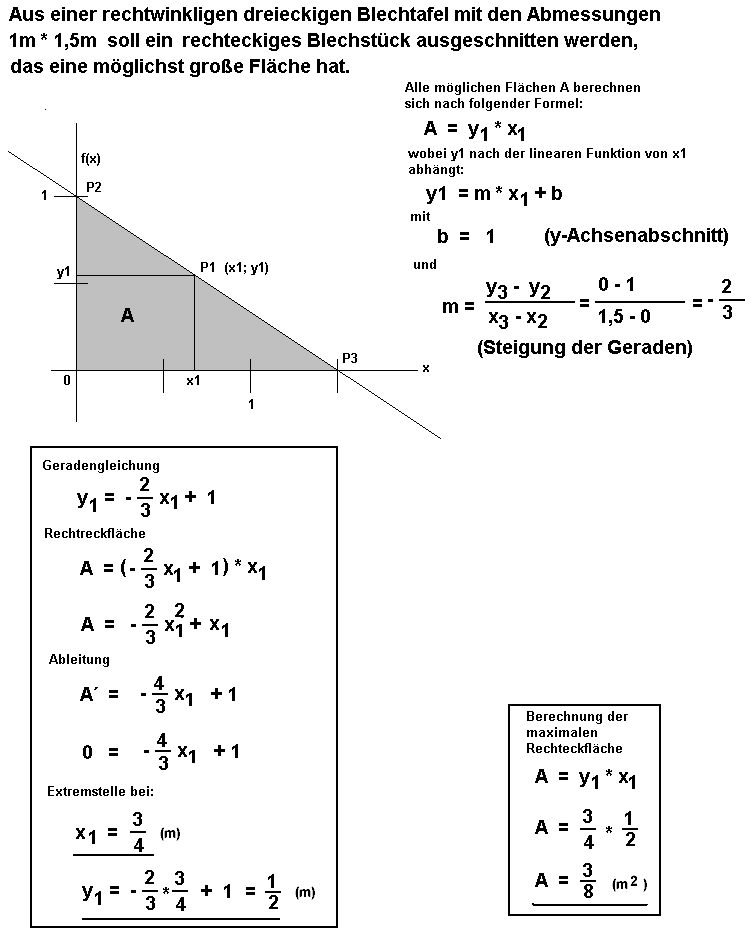

6. Aufgabe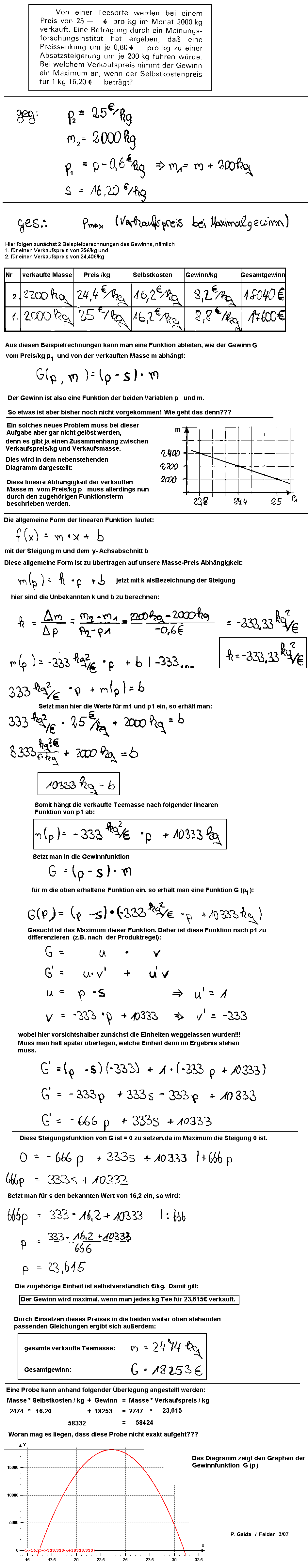

7. Aufgabe

8. Aufgabe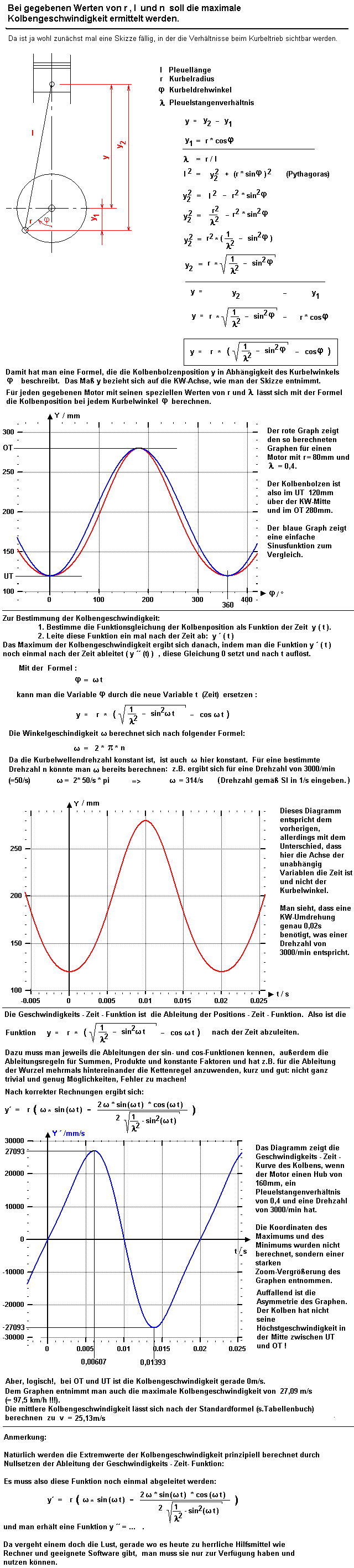

9. Aufgabe

10. Aufgabe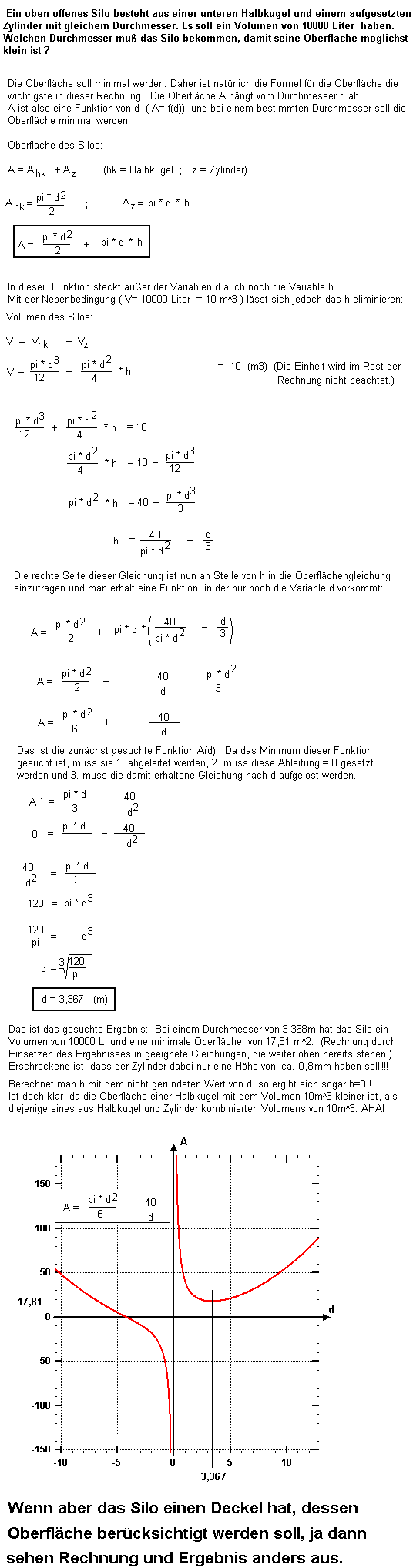

11. Aufgabe

12. Aufgabe

13. Aufgabe

14. Aufgabe

15. Aufgabe

16. Aufgabe

17. Aufgabe

Gegeben ist eine gekrümmte Fläche über / unter der x-y-Ebene.
Sowohl die Fläche als auch das unter der Fläche befindliche Volumen hängen ab von der Länge l ab.
Beide Funktionen [A(l) und V(l)] sind ganzrationale Funktionen.
Die Fläche A hat ein Maximum von 100 bei l = 10.
Das Volumen V hat ein Maximum von 1000 bei l = 20.
Außerdem soll gelten V= 10 * A * l

Ermitteln Sie die Funktionsterme für A(l) und V(l).

Lösung:
Mit den Angaben zum Flächenmaximum und Volumenmaximum hat man insgesamt 4 Informationen zur Verfügung:
1. Bei l1= 10 ist A1 = 100
2. Bei l2 = 100 ist V2 = 1000
3. Bei l1 liegt ein Flächenmaximum vor (Bei l1 hat der Graph A(l) eine horizontale Tangente)
4. Bei l2 liegt ein Volumenmaximum vor (Bei l2 hat der Graph V(l) eine horizontale Tangente)

Aus diesen 4 Informationen lassen sich 4 Gleichungen bilden:
1. A(10) = 100
2. V(20) = 1000
3. A´(10) = 0
4. V´(20) = 0

Mit 4 Gleichungen lassen sich 4 Unbekannte berechnen.
Da A(l) und V(l) jeweils ganzrationale Funktionen sein sollen, muss eine der beiden Funktionen 3. Grades sein ( 4 unbekannte Parameter).
Der Grad von V(l) ist eins größer als der Grad von A(l) (s. Aufgabenstellung).
Daher wird angenommen A(l) sei eine Funktion 3. Grades.

Die allgemeinen Gleichungen lauten somit:
A = al^3 + bl^2 + cl +d
V = 10al^4 + 10bl^3 + 10cl^2 + 10dl
A´= 3al^2 + 2bl + c
V´= 40al^3 + 30bl^2 + 20cl + 10d

Die bekannten Werte einsetzen, ergeben sich die 4 konkreten Gleichungen I ...IV:

I      1000a +   100b +   10c +    d =  100
II  1600000a + 80000b + 4000c + 200d = 1000
III     300a +    20b +     c        =    0
IV   320000a + 12000b +  400c +  10d =    0

Ein Gleichungssystem aus 4 Gleichungen mit 4 Unbekannten ist zu lösen.
Bei einem Gleichungssystem aus 3 Gleichungen mit 3 Unbekannten kann der Taschenrechner helfen.
Daher wird dieses 4er Gleichungssystem zunächst "zu Fuß" reduziert auf ein System mit 3 Gleichungen.
Dazu wird Gleichung III umgestellt nach c und das so erhaltene Ergebnis in die anderen Gleichungen eingesetzt.
Aus III folgt: c = -300a - 20b.
Einsetzen in Gl I, II und IV ergibt:

   1000a +   100b +   10(-300a - 20b) +    d =  100
1600000a + 80000b + 4000(-300a - 20b) + 200d = 1000
 320000a + 12000b +  400(-300a - 20b) +  10d =    0

Klammern auflösen und zusammenfassen ergibt:

- 2000a -  100b +    d =  100
400000a         + 200d = 1000
200000a + 4000b +  10d =    0

Dieses Gleichungssystem löst ein Taschenrechner flugs zu:
a = 0,1875; b = -8,45; d = -370
Mit der Gleichung III lässt sich nun c berechnen zu:
c = 112,8

Mit den nun gefundenen 4 Parametern ergeben sich die gesuchten Funktionsgleichungen zu:

A(l) = 0,1875l³ - 8,45l² +112,8l - 370
V(l) = 1,875l⁴ -84,5l³ + 112,8l² -3700*l

Oh Schreck !!!
Alles ok
Nur bei x = 20 hat V ein Minimum statt ein Maximum!!
Wie muss der Rechenweg geändert werden, um das erwartete Maximum zu garantieren?

18. Aufgabe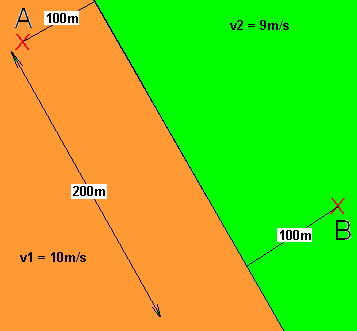

Ein Elektrobuggy steht in Punkt A und will nach Punkt B. Punkt A liegt auf Asphalt (braune Oberfläche), während Punkt B auf einer Wiese (grüne Oberefläche) liegt. Auf Asphalt kann der Buggi mit v1 = 10m/s schnell fahren, dagegen auf der Wiese nur mit v2=9m/s. Die Entfernungen in Meter sind in der Skizze angegeben.

Gesucht ist der schnellste Weg von A nach B.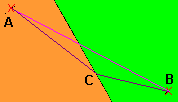

Der kürzeste Weg ist natürlich die gerade Verbindungslinie von A nach B.
Vermutlich ist dies aber nicht die schnellste Möglichkeit. Besser ist es sicher, einen etwas größeren Weg auf dem Asphalt zurückzulegen als auf der Wiese.
Es muss also auf der Grenzlinie der beiden Oberflächen einen Punkt (nennen wir ihn) C geben, der etwas unterhalb vom Schittpunkt der geraden Verbindungslinie mit der Grenzlinie liegen muss, bloß wo genau?

Diese Aufgabe ist eine hübsche Extremwertaufgabe. Es soll ein Weg gefunden werden, der die minimale Fahrzeit garantiert. Es ist also eine kleine Physikaufgabe mit den physikalischen Größen Weg (s), Zeit (t) und Geschwindigkeit (v).

Benötigt wird nur die Grundformel t = s/v, ein wenig Geometriekenntnis und natürlich Fertigkeiten in der Differenzialrechnung.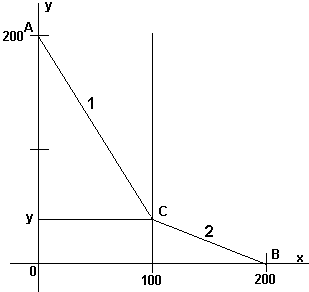

Ortsskizze AB mit Weglinien im Koordinatensystem

Um die Aufgabe mathematisch verdaulich zu gestalten, zeichnet man die Skizze anders, verdreht sie ein wenig und trägt die Ortsverhältnisse in ein Koordinatensystem ein.

So lässt sich leicht erkennen, dass der schnellste Weg aus 2 Teilstücken besteht.

Es gilt natürlich:

   s_ges = s₁ + s₂

   t₁   = s₁ / v₁

   t₂   = s₂ / t₂

   t_ges = t₁ + t₂

   t_ges = s₁ / v₁ + s₂ / t₂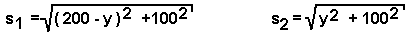

Die Teilstrecken s₁ und s₂ sind mit dem PYTHAGORAS zu berechnen.

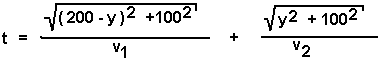Funktionsterm tges=f(y)

Dies wird eingesetzt in die Formel für die Gesamtzeit und man erhält einen Term für die Gesamtzeit als Funktion von y.
Da t ein Minimum werden soll, ist diese Funktion nun nach y abzuleiten, gleich 0 zu setzen und aus der so erhaltenen Formel y zu berechnen.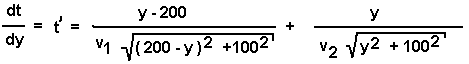

Funktionsterm tges=f(y)

Für dieses Ergebnis benötigt man u.a. die Potenzregel. die Summenregel, die Kettenregel, die Ableitung der Wurzel und noch Fähigkeiten im Kürzen von Brüchen.

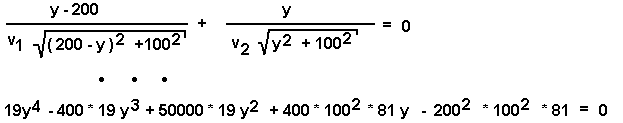Funktionsterm tges=f(y)

viel Schweiß, stundenlange algebraische Umformungen (9./10. Schuljahr) viele Fehler und Korrekturen und viel Kaffee, Kekse und Schokolade führten schließlich auf die Lösungsformel:

Sie sollten solange an der Aufgabe herumbasten, bis Sie diese Formel auch gefunden haben!! (Das gleiche gilt natürlich auch für die Ableitung.)

Eine solche Plynomformel 4. Grades ist herkömmlich nicht mehr zu lösen.
Entweder Sie tun´s mit Näherungsverfahren (s. Buch), mit Excel, mit einem Funktionsplotter (z.B. wzgrapher) oder mit einem geeigneten Taschenrechner (Solver-Funktion).

Alle Methoden ergeben die Lösung :

y = 89,559

Setzt man diesen Wert für y noch in den Funktionsterm für t_ges ein, so erhält man

t_ges = 29,814 s

Das Licht macht diese Berechnung zwar nicht, findet aber irgendwie selbständig den schnellsten Weg, wenn es zu einem Ziel soll und unterwegs der Lichtstrahl plötzlich durch ein anderes Medium mit einer kleineren Lichtgeschwindigkeit muss.(z.B. knickt der Lichtstrahl ab, wenn er schräg aus der Luft ins Wasser taucht. Und das tut er genau nach diesen Berechnungen. s. Lichtbrechung.)

Die gestellte Aufgabe lässt sich also auch lösen, indem man das Brechungsgesetz für Licht anwendet. Man spart auf diese Weise die Differenziation, kommt aber auf eine ähnliche Formel wie die, die noch mit viel Schweiß ... zur Lösungsformel umgestellt werden muss. Schließlich erhält man dasselbe Ergebnis. (Brechungsgesetz : sin(alpha) / sin(beta) = v1/v2)

19. Aufgabe

Jeder Zylinder eines 4-Zylinder-Motors habe einen Hubraum von 500 cm^3.
Der Verdichtungsraum im Zylinderkopf soll ebenfalls zylinderförmig sein.
Das Verdichtungsverhältnis ist 11:1.

Bestimmen Sie den Hub und die Bohrung so, dass die Gesamtoberfläche des Zylinders minimal wird, damit möglichst wenig Wärmeverlust auftritt.
Wie groß ist dann die Gesamtoberfläche?

Lösungsweg:

Skizze malen, Werte eintragen, erforderliche Formelzeichen eintragen

Formel für Hubraum, Verdichtungsraum, Verdichtungsverhältnis notieren.

Gesamtvolumen berechnen (550cm^3)

Formel für Zylinderoberfläche notieren (allgemein, diese Formel enthält die beiden Variablen r bzw. d und h.)

Da das Volumen bekannt ist, kann und muss h ersetzt werden durch V und r!

Nun liegt eine Funktion O = f(r) vor.

Differenzieren (dO/dr = O´= .... )

O´ = 0 setzen.

Formel nach r auflösen (r= 4,44 cm)

h berechnen ( h= 8,88cm , Gesamthöhe von Zylinder + Zylinderkopf)

s berechnen (s = 8,07 cm)

Probe: Vh = 500cm^3

Gesamtoberfläche berechnen O = 371,6 cm^2

20. Aufgabe

Spieltrieb
Cogito
Eine Knobelei für clevere Leser von Heinrich Hemme, Professor für Physik an der Fachhochschule Aachen

Knobeln in Vorpommern

Ich hatte einen Termin bei einer Firma in Anklam an der Peene und machte mich am späten Nachmittag auf den Rückweg. Auf der A20 mitten in Vorpommern streikte mein Auto. Ein gelber Engel vom ADAC schleppte es zur nächsten Werkstatt in einem kleinen Ort in der Nähe von Greifswald. ,,Tja", sagte der Meister. ,,Den kriege ich schon wieder flott, aber nicht mehr heute. Morgen früh um zehn können Sie ihn abholen." Zum G1ück gab es in dem Ort einen Landgasthof mit ein paar Fremdenzimmern. ,,Die Küche schließt um neun", sagte der Wirt, als er mir den Zimmerschlüssel gab. Ich wusch mich rasch und ging in die Gaststube. Die Speisekarte war sehr übersichtlich, und ich konnte mich nur zwischen drei verschiedenen Schnitzelgerichten entscheiden. ,,Nachtisch gibt es nicht", sagte der Wirt, als er abräumte. Also setzte ich mich an die Theke, wo schon zwei Männer hockten und schweigend ihr Bier tranken. ,,Jan, gib mal den Knobelbecher rüber", sagte einer der beiden zum Wirt und fragte mich dann: ,,Machst du mit? Wir spielen über 30 Runden. Wer die meisten Runden verliert, zahlt alle Deckel." Ich wollte nicht unhöflich sein und willigte ein. ,,Die Regeln sind ganz einfach. Geknobelt wird mit einem Würfel. Du entscheidest dich vorher, wie viele Würfe pro Runde du machen willst. Diese Entscheidung gilt für den ganzen Abend, und du kannst sie nicht mehr ändern. Die Augenzahlen deiner Würfe in einer Runde werden zusammengezählt. Auch von uns entscheidet sich jeder für eine Wurfzahl pro Runde.

Wer in einer Runde die wenigsten Augen geworfen hat, hat sie verloren. Hast du das so weit verstanden?" Ich nickte. ,,Es gibt aber noch einen kleinen Haken", ergänzte der andere Mann. Wenn du eine 1 würfelst, verfallen deine bisher erworbenen Augen und die Runde endet für dich sofort mit null Punkten. Also: Wie oft willst du würfeln?" Ich überlegte nicht lange und sagte: ,,13 Mal." Meine Mitspieler nannten auch jeder eine Zahl, und dann begannen wir.

Der Wirt und die beiden Männer waren offensichtlich der Ansicht, dass damit alles gesagt sei, denn in den nächsten zwei Stunden fiel kaum noch ein Wort. Dafür aber wurde umso mehr Bier getrunken. Meine Entscheidung, pro Runde 13 Mal würfeln zu wollen, war wohl nicht optimal gewesen. Denn meistens gewann einer meiner Mitspieler. Gegen e1f Uhr waren dann die 30 Runden beendet, und ich hatte mit Abstand am häufigsten verloren. Wortlos schoben die beiden Männer mir ihre Bierdeckel zu, sagten ,,Tschüss" und verließen den Gasthof. A1s ich die drei Bierdeckel bezahlt hatte und auf mein Zimmer ging, fragte ich mich, für welche Zahl von Würfen pro Runde ich mich hätte entscheiden müssen, damit ich die höchstmögliche Chance zu gewinnen gehabt hätte. Aber mein Verstand war vom Bier zu sehr getrübt, um das herauszubekommen. Wissen Sie es?

bild der wissenschaft 6-2015

Lösungsweg:

Welche Augengesamtsumme kann man erwarten, wenn man (z.B.) 10000 mal würfelt?.

Wie groß ist dann also die durchschnittlich gewürfelte Augenzahl?

Wie sieht´s aus, wenn man alle gewürfelten Einser weder bei der Wurfanzahl noch bei der Augenzahl berücksichtigt?

Wie groß ist die Wahrscheinlichkeit, bei einem Wurf eine Eins zu würfeln?

Wie groß ist die Wahrscheinlichkeit, bei einem Wurf KEINE Eins zu würfeln?
Denn: Wenn man bei diesem Spiel die erste EINS gewürfelt hat, bekommt man für diese Runde 0 Punkte (PECH!).

Wie groß ist die Wahrscheinlichkeit, bei (z.B.) 10 Würfen KEINE Eins zu würfeln?
Dazu muss man wissen, dass sich diese Gesamtwahrscheinlichkeit aus dem Produkt der Einzelwahrscheinlichkeiten ergibt.

Den sogenannten ERWARTUNGSWERT (durchschnittliche Augenzahl pro Spielrunde) erhält man durch Multiplikation der durchschnittlichen Augenzahl bei x mal Würfeln, wenn die 1 nicht mitzählt und der Wahrscheinlichkeit, bei x Würfen KEINE 1 zu würfeln. (ALLES KLAR?)

Damit hat man eine Formel gefunden, wo der Erwartungswert von der Wurfzahl abhängt. Differenzieren , Ableitung = 0 setzen, Formel nach x auflösen, halt das Übliche Verfahren.

Ergebnis: x=5,48

Nun muss man sich nur noch zwischen 5 ODER 6 Würfen pro Runde entscheiden! Tun Sie´s nun.

Die Abbildung zeigt den zugehörigen Funktionsgraphen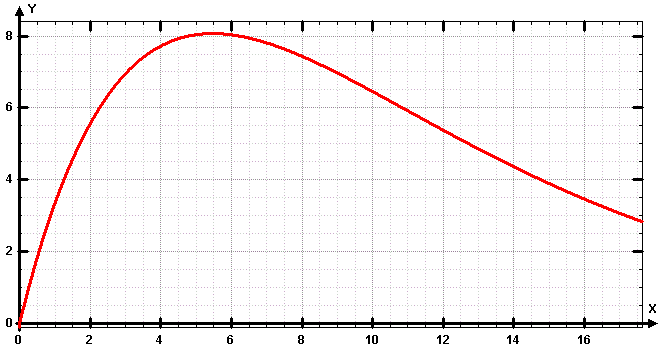
Funktionsgraph 4x(5/6)^x

Hier sind einige Links zu finden, die zu interessanten / hilfreichen Matheseiten im WWW führen.

www.kszofingen.ch	interaktive Mathetests
www.mathe-online.at
www.ies.co.jp	engl. Mathe-Java-Applets
mathenexus.zum.de
www.arndt-bruenner.de
mathematik.zum.de
www.tutorvista.com	kostenpflichtige Nachhilfe weltweit jederzeit