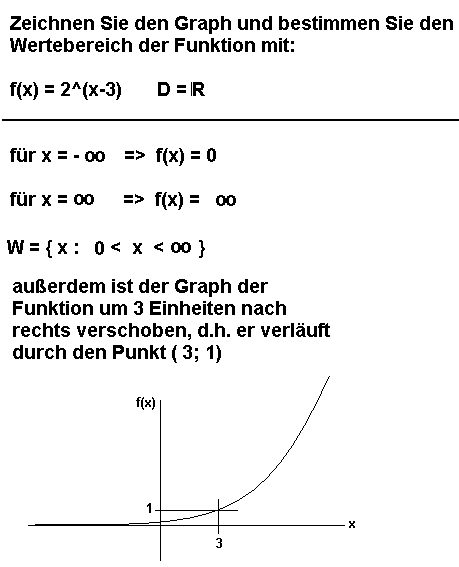
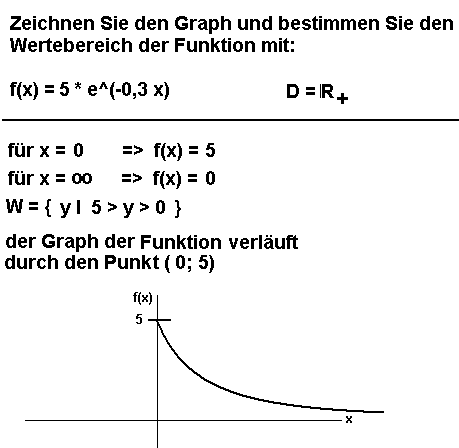
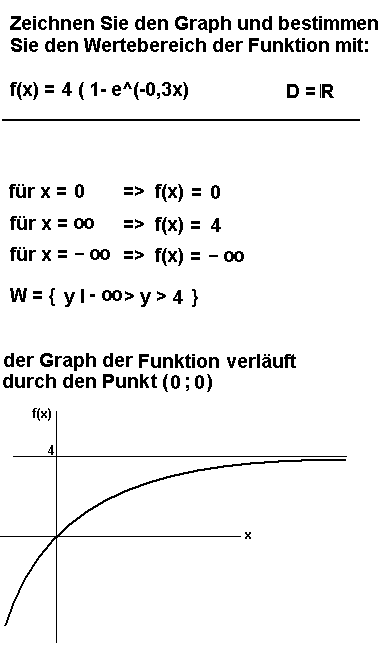
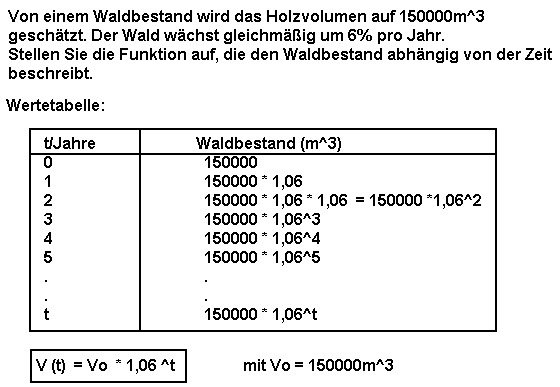
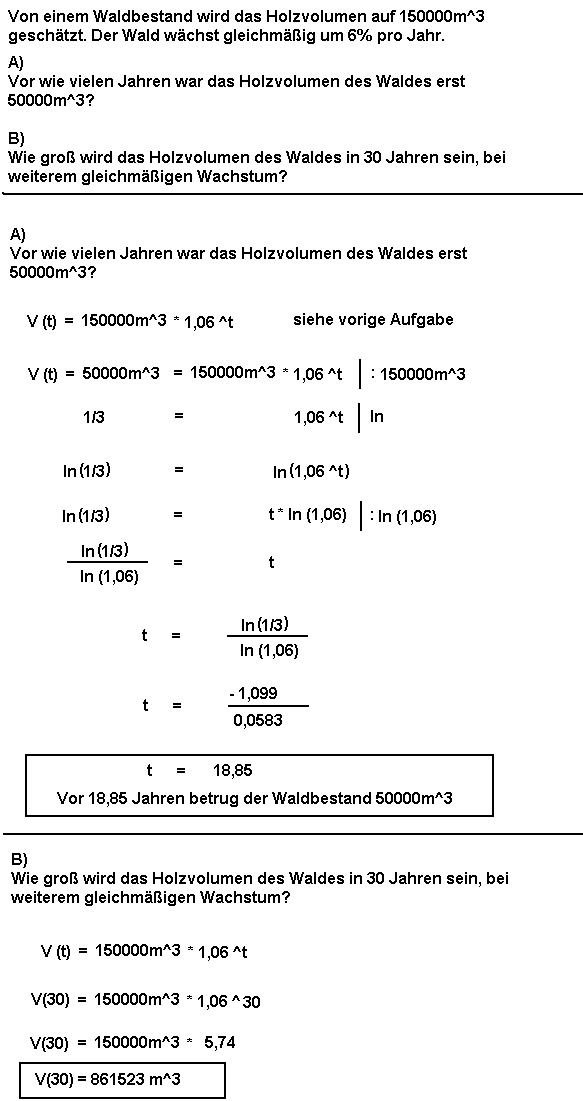
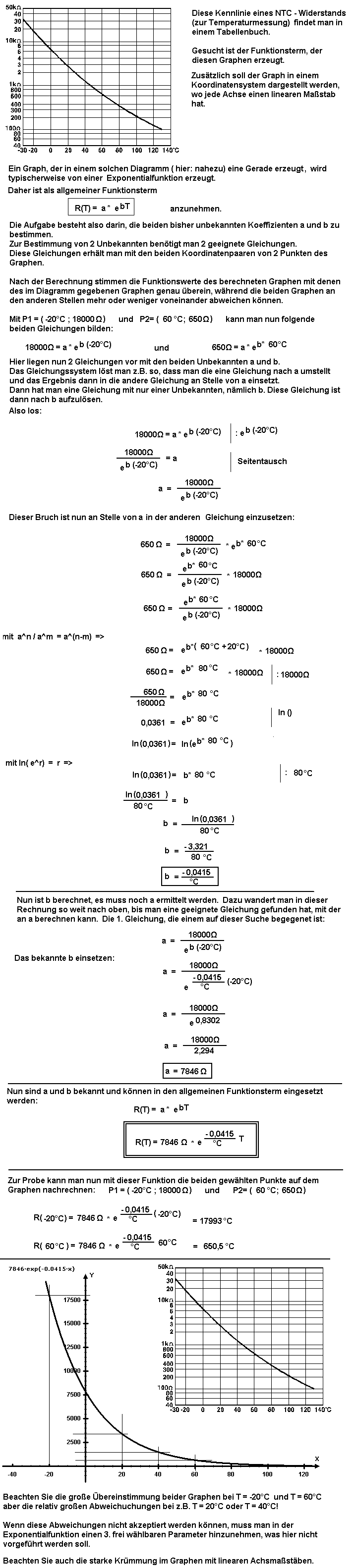
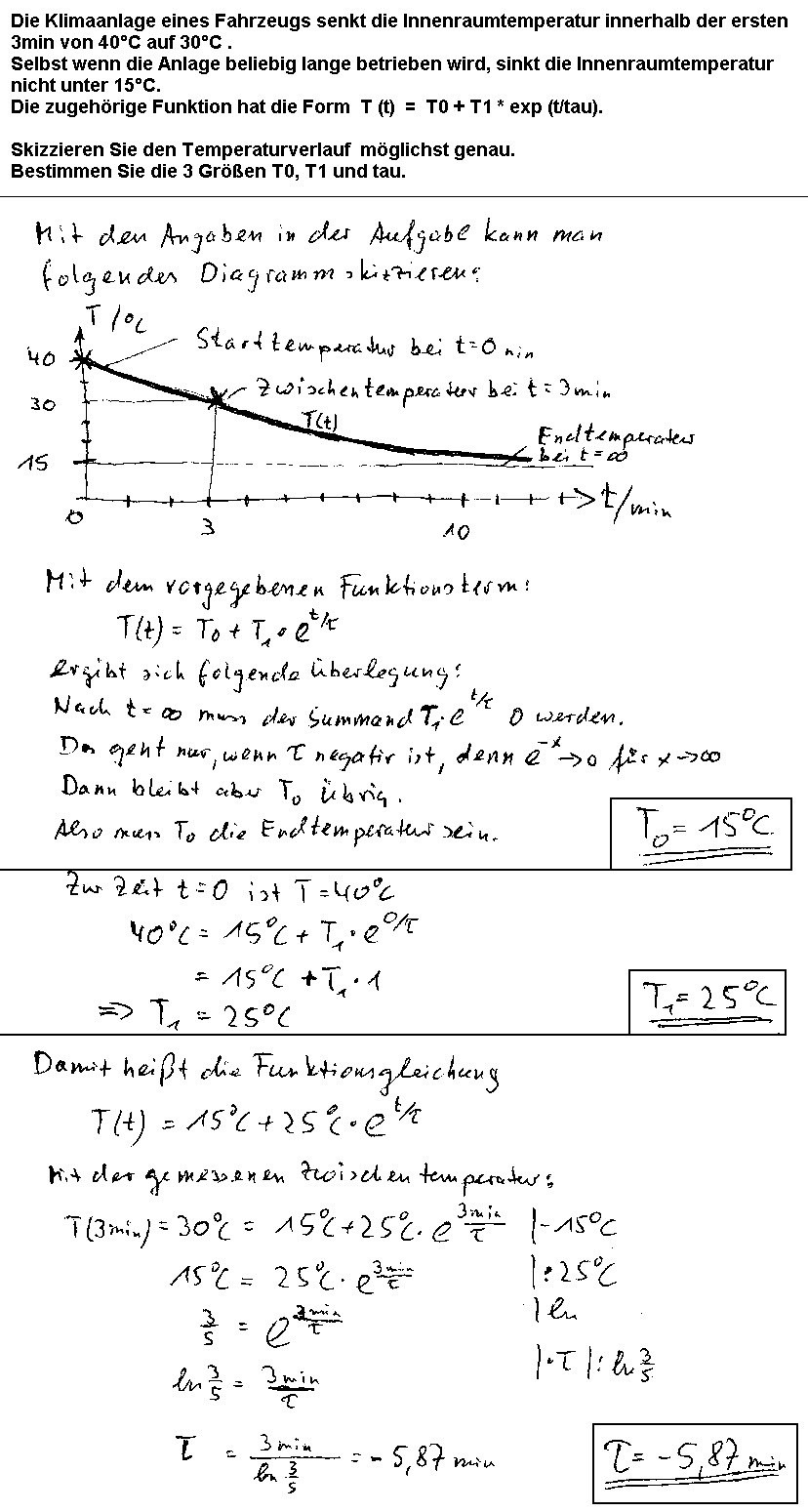
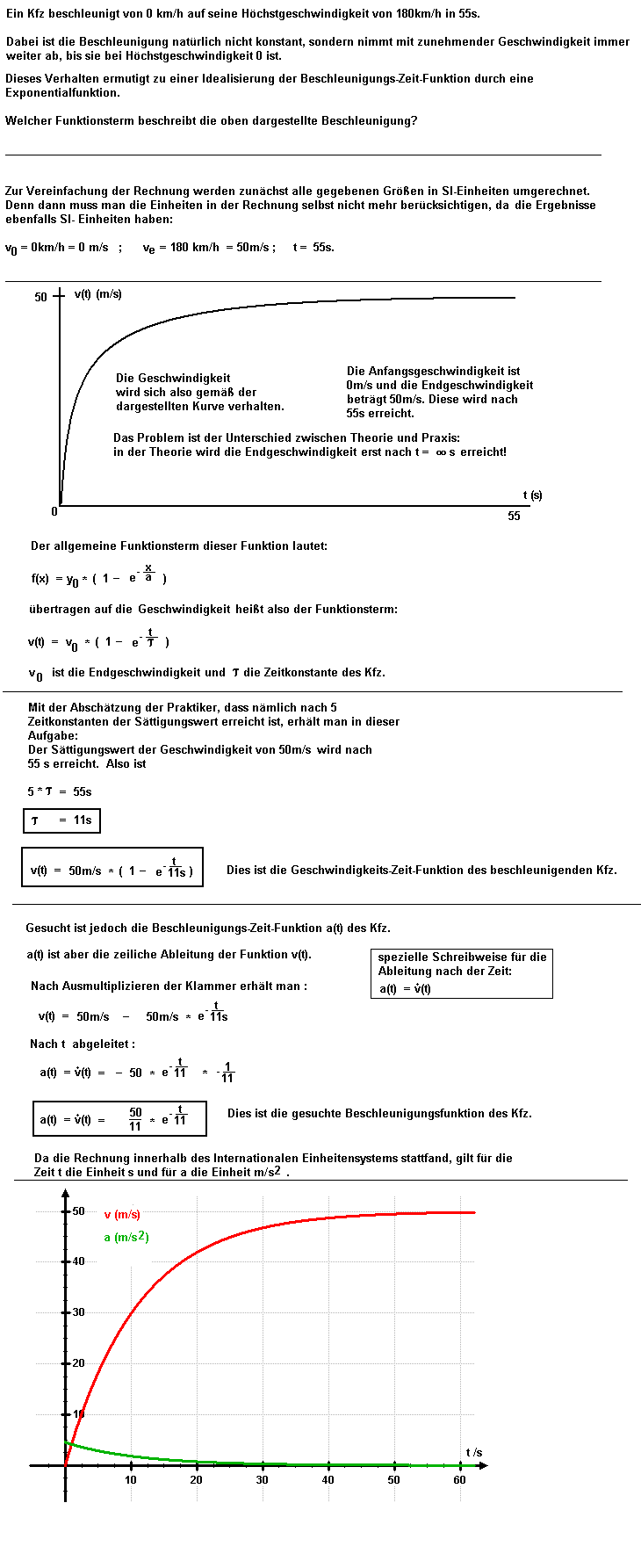
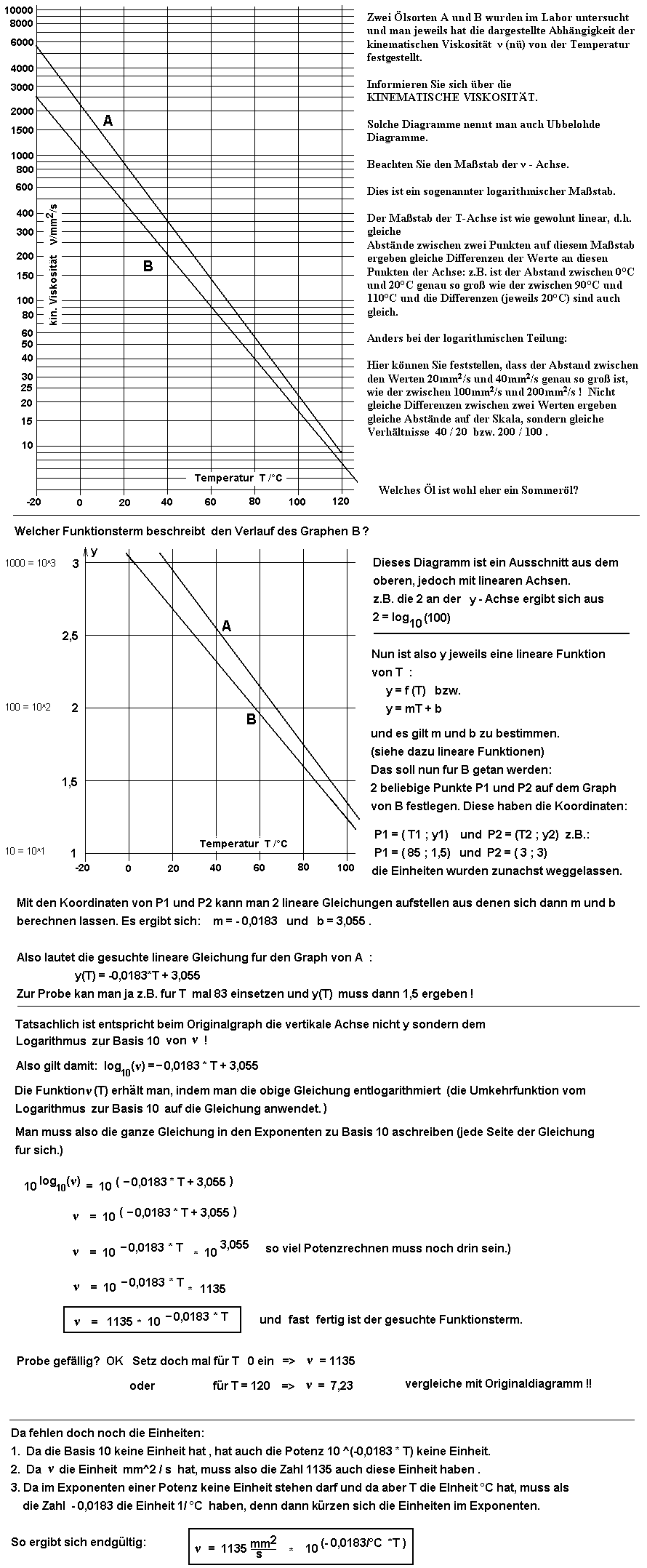
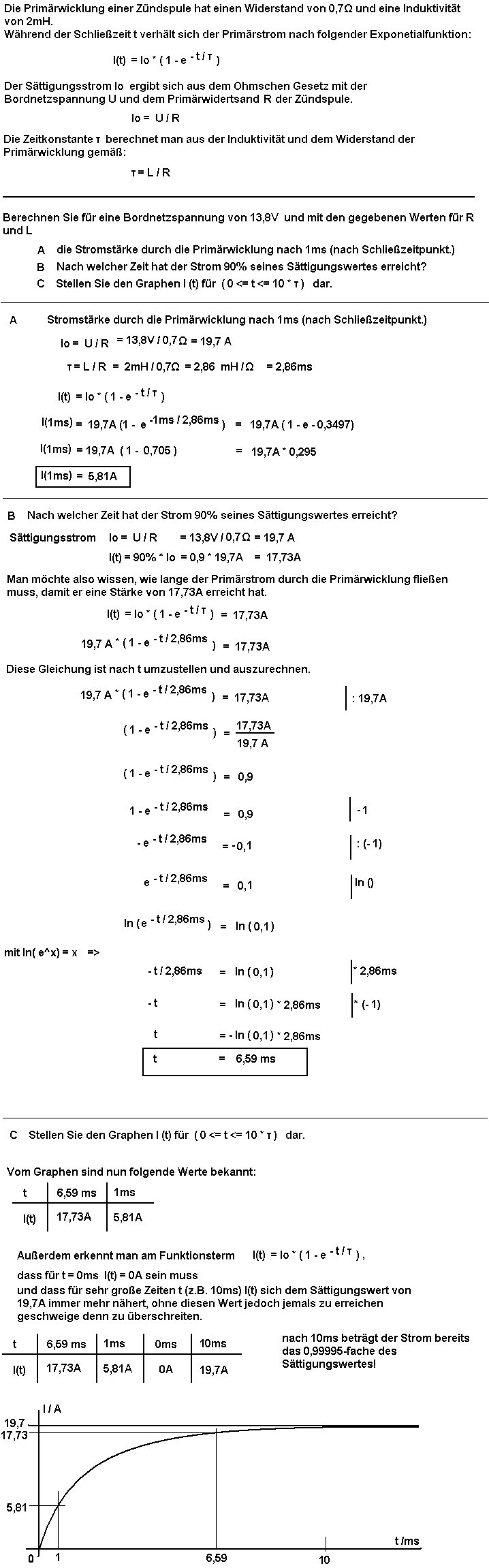15. Aufgabe
Für die Primärwicklungen der Zündspulen eines
- 3-Zylinder-4-Takt-Ottomotors mit
-
Einzelfunkenspulen,
-
einer Höchstdrehzahl von 6000/min,
-
Schließwinkelsteuerung (10% <= α <= 90%),
-
R1 = 0,75Ω (Primärwicklungswiderstand),
-
UBatt = 13,5V (Bordnetzspannung),
-
Emin = 30mJ (Mindestenergie, die in der Zündspule zum ZZP gespeichert sein muss)
soll deren erforderliche Induktivität L so berechnet werden, dass auch im ungünstigsten Fall zuverlässig die Zündungen ausgelöst werden.
Zur Lösung dieser Aufgabe benötigt man Einiges an Wissen, was aber am Ende des 2. Ausbildungsjahres zum Kfz-Mechatroniker normalerweise vorausgesetzt werden kann:
- Funktion eines Ottomotors,
-
Funktion einer Zündanlage,
-
Begriff des Schließwinkels,
-
Formel zur Berechnung der Energie einer stromduchflossenen Spule:
E = 1/2 L I2
-
Bedeutung der üblichen Formelzeichen der Kfz-Technik und der Elektrotechnik,
-
Formel für das zeitliche Verhalten des Stromes durch eine Spule nach seinem Einschalten:
I(t) = I0 * ( 1 - e(-t/τ) )
-
Formel zur Berechnung der Zeitkonstanten τ der Primärwicklung:
τ = L / R
-
Ein paar Fähigkeiten und Tricks aus der Mathematik und Beherrschung eines technisch wissenschaftlichen Taschenrechners
.
So, nun genug Angst und Schrecken eingejagt! So völlig unmöglich ist die Lösung der Aufgabe auch wieder nicht.
Dabei wird die Lösung hier nicht in allen Einzelheiten präsentiert, sondern es werden nur die groben Schritte und einige Zwischenlösungen dargestellt:
|
Der ungünstigster Fall liegt dann vor, wenn die Zündspule am wenigsten Zeit zur Verfügung hat, Energie zu speichern:
|
maximale Motordrehzahl: nmax = 6000/min
|
In diesem Fall wird die Schließwinkelsteuerung für den maximalen Schließwinkel sorgen:
αmax = 90% (Wovon denn nur?)
| |
Mit den gegebenen Daten erhält man für diesen ungünstigsten Fall eine Schließzeit von
|
t = 0,018s
|
Diese Zeit steht also der Primärwicklung mindestens zur Verfügung, um genug Energie für den nächsten Zündfunken zu speichern.
Das Steuergerät schaltet also dann genau 0,018s vor dem ZZP den Primärstrom ein und zum ZZP wieder ab.
Damit hat man aber bereits den Wert für t gefunden, der in dem Funktionsterm für I(t) eine Rolle spielt.
| |
Die in der Primärwicklung gespeicherte Energie hängt ab von
|
1. der Induktivität L der Primärwicklung (konstant)
|
2. vom Strom I, der gerade zum ZZP durch die Primärwicklung fließt.
| |
Da aber der Strom durch die Primärwicklung eine Funktion der Zeit ist,
|
und da die Energie vom Stromfluss abhängt,
|
ist also auch die Energie in der Primärwicklung eine Funktion der Zeit und es gilt:
E(t) = 1/2 L I(t)2
bzw. wenn man den Funktionsterm für I(t) einsetzt:
E(t) = 1/2 L (I0 * ( 1 - e(-t/τ) ))2
| |
Ersetzt man in der Funktion τ durch L / R
|
so erhält man:
|
E(t) = 1/2 L (I0 * ( 1 - e(-t*R/L) ))2
|
I0 ist der Sättigungsstrom, der dann durch die Primärwicklung fließt, wenn t >> τ
>> : sehr viel größer als
|
In dem Fall ist die Energiespeicherung abgeschlosen und die Spule setzt dem Stromfluss nur noch ihren ohm´schen Widerstand entgegen.
|
I0 = UBatt / R1 = 18 A
| |
Setzt man nun in den Funktionstern E(t) alle bekannten Werte ein,
|
so erhält man:
|
0,03J = 1/2 L (18A * ( 1 - e(-0,018s*0,75Ω/L) ))2
oder, wenn man zusammenfasst und die Einheiten mal weglässt (SI):
0,03 = 162 * L * ( 1 - e(-0,0135/L) ))2
|
Na Prima!
|
Da wurde also eine Formel entwickelt, in der als einzige Unbekannte nur noch L vorkommt.
|
Nur: Wie man diese nach L umstellt, ist mir nicht bekannt!!
| |
Also: andere Lösungsmöglichkeiten
|
grafische Lösung (Funktionsplotter)
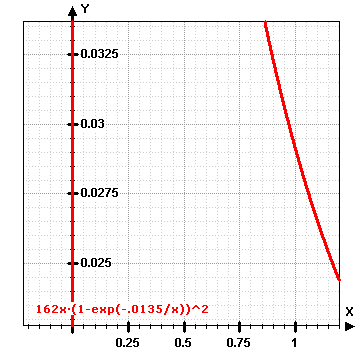
Das Diagramm zeigt einen Ausschnitt des Graphen der Funktion:
f(x) = 162x * (1- exp(-0,0135/x))^2
Diese Funktion erhält man aus der rechten Seite der Formel, wenn man L durch x ersetzt.
Dann lässt sich dem Plot entnehmen, dass der Graph im angezeigten Ausschnitt 2 mal den Wert 0,03 hat, nämlich bei
x1 ungefähr 0 und bei x2 ungefähr 0,95.
Durch genaueres Zoomen erhält man:
x1 =0,000185 und x2= 0,97
|
Taschenrechner
(Man hat nicht immer einen Funktionsplotter zur Hand!)
Mit der SOLVER - Funktion einiger Taschenrechner lassen sich Nullstellen mit für praktische Zwecke meist genügender Genauigkeit finden:
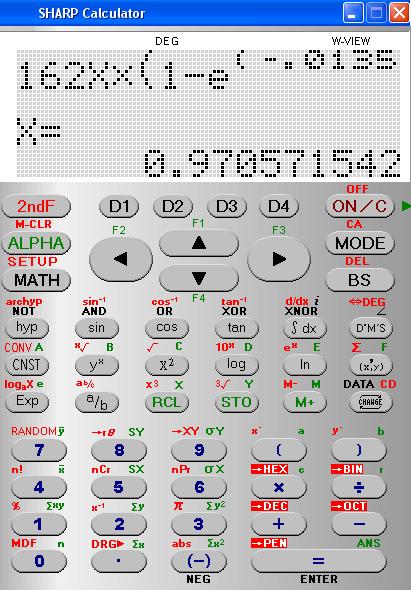
- Formel so umstellen, dass rechts vom "="-Zeichen eine 0 steht.
- Formel in den TR eingeben und speichern.
- Solver-Funktion aufrufen.
- verschiedene Start- und dx-Werte probieren.
- Mit etwas Glück und Überlegung erhält man ebenfalls die beiden Lösungen:
x1 =0,000185... und x2= 0,9705...
- Mit viel Pech erhält man immer nur die Fehlermeldung ERROR CALCULATION!!
|
| |
Die zugehörige Einheit ergibt sich aus dem internationalen Einheitensystem, innerhalb dessen diese Kalkulation ablief.
|
[L] = H (Henry)
1H = 1Vs/A
|
Also muss die Primärwicklung entweder eine Induktivität von
L1 = 0,97H
oder aber von
L2 = 0,185mH
haben.
| |
Probe !!
|
für L1:
τ1 = 0,247ms
I(t)1 = 0,25A
E1 = 0,03J
|
für L2:
τ2 = 1293ms
I(t)2 = 18A
E2 = 0,03J
|
|
16. Aufgabe
Zur Bestimmung des Funktionsterms für einen bestimmten Funktionsverlauf kann man in
einer Exponentialfunktion eine beliebige Basis wählen.
Dies soll hier nicht allgemein bewiesen, aber immerhin an einem Beispiel mit 2 verschiedenen Basen
demonstriert werden.
f1(x) = 5* 23x
Wie muss der Funktionsterm lauten, wenn nicht 2 sondern 10 als Basis gewählt wird, aber die Grafen beider Funktionen deckungsgleich sein sollen?
Zunächst ein allgemeiner Ansatz. Die konkreten Zahlenwerte (5 und 3) aus f1(x) werden durch allgemeine Symbole (a und b)
für f2(x) ersetzt, denn diese Werte müssen doch wahrscheinlich der neuen Basis angepasst werden (andere Parameter zur Anpassung stehen nicht zur Verfügung).
f2(x) = a* 10bx
Die weiteren Überlegungen folgen:
f1(0) = 5. Also muss auch f2(0) = 5 sein, schließlich sollen die beiden Grafen ja kongruent sein.
Daraus folgt, dass a = 5 sein muss. Hier gab´s offenbar nix anzupassen.
Damit hat man also :
f2(x) = 5* 10bx
Die Unbekannte b muss noch berechnet werden. Dazu betrachtet man einen beliebigen anderen x-Wert, z.B. x= 1 (möglichst einfach).
f1(1) = 5* 23*1 = 5 * 8 = 40
Wieder gilt, dass natürlich auch f2(1) = 40 sein muss, also
f2(1) = 5* 10b*1 = 40
Dies ist nun die Bestimmungsgleichung für b. Wenn man zunächst durch 5 dividiert, erhält man:
10b*1 = 8
Nun wird auf beiden Seiten logarithmiert. Hier bietet sich der log (Basis 10) an:
b= log(8) = 0,9031
Damit erhält man den gesuchten Funktionsterm:
f2(x) = 5* 100,9031x
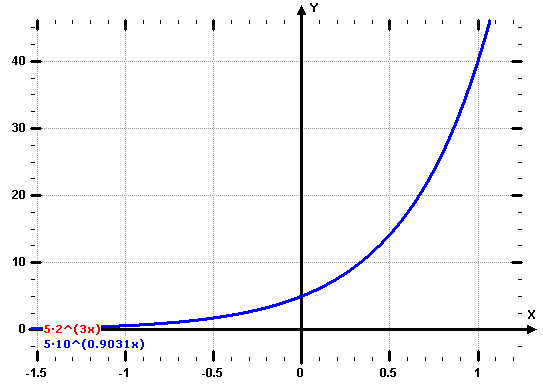Die Grafik zeigt nur einen Funktionsgraf. Der rot gezeichnte wird vom blau gezeichneten total überdeckt.
Außerdem erkennt man, dass beide Grafen durch die beiden Punkte (0 ; 5) und (1 ; 40) verlaufen.
|
|
17. Aufgabe
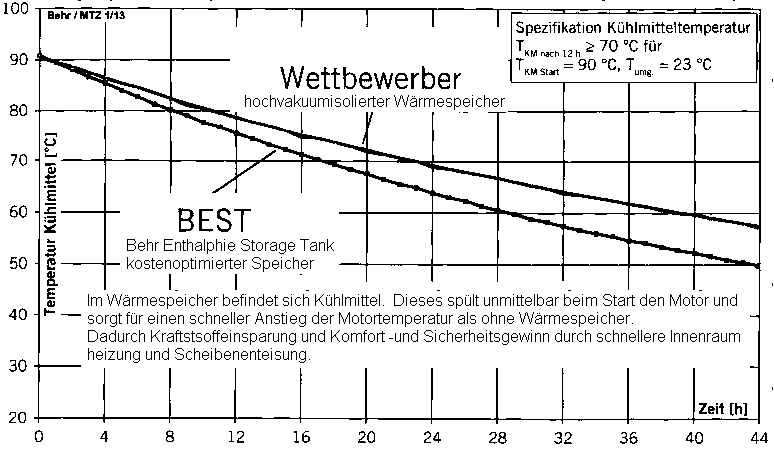
Firma Behr entwickelt einen kostengünstigen Wärmespeicher (Thermoskanne) für Kühlwasser und testet wie schnell
das gespeicherte Kühlmittel abkühlt.
Zum Vergleich dient ein anderer Wärmespeicher, der hochvakkumisoliert ist, deswegen zwar die Wärme besser hält aber wesentlich teurer ist.
Die im Experiment ermittelten Abkühlkurven zeigt das Schaubild.
Aufgabe:
Bestimmen Sie für den BEST Wärmespeicher den Funktionsterm T=f(t)
Hinweise:
- Skizzieren Sie den Temperaturverlauf für einen Zeitraum von 1 Woche. Beachten Sie dabei alle Angaben im Schaubild.
- Der Funktionsterm muss die Form T(t) = A * eBt + C haben.
- A, B, C sind die unbekannten Parameter und müssen ermittelt werden.
- Um 3 unbekannte Größen zu berechnen braucht man 3 geeignete Gleichungen.
- Die 3 Gleichungen bekommt man durch die Koordinaten von 3 beliebigen Punkten des Graphen.
- Durch geschickte Wahl der 3 Punkte kann man eine Menge Arbeit sparen.
- Wählen Sie t1=0, t3= unendlich, t2 beliebig zwischen t1 und t3
- Lösung: T(t)= 67°C * e-0,0201t + 23°C
- Berechnen Sie als Proben die Temperaturwerte bei t1, t2 und t3.
- andere Probemöglichkeit: stellen Sie in Excel den Funktionsgrafen dar.
|
|
18. Aufgabe
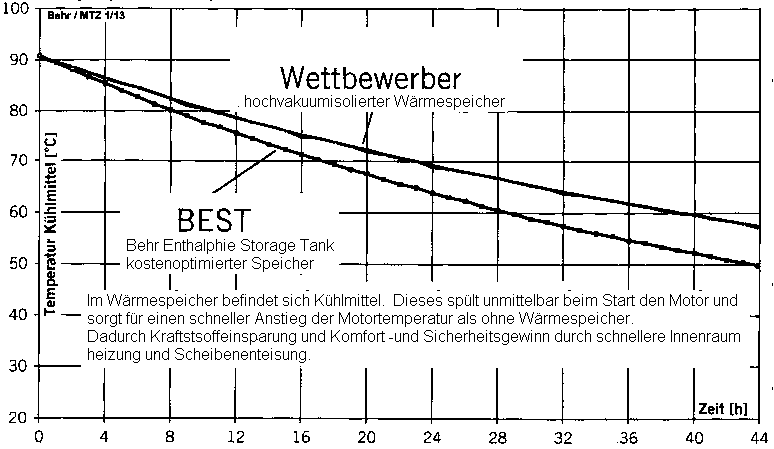
Firma Behr entwickelt einen kostengünstigen Wärmespeicher (Thermoskanne) für Kühlwasser und testet wie schnell
das gespeicherte Kühlmittel abkühlt.
Zum Vergleich dient ein anderer Wärmespeicher, der hochvakkumisoliert ist, deswegen zwar die Wärme besser hält aber wesentlich teurer ist.
Die im Experiment ermittelten Abkühlkurven zeigt das Schaubild.
Aufgabe:
Bestimmen Sie für den BEST Wärmespeicher den Funktionsterm T=f(t)
Hinweise:
- Die Aufgabe unterscheidet sich von Aufgabe 17 durch Fehlen einer wesentlichen Information!
- Der Funktionsterm muss die Form T(t) = A * eBt + C haben.
- A, B, C sind die unbekannten Parameter und müssen ermittelt werden.
- Um 3 unbekannte Größen zu berechnen braucht man 3 geeignete Gleichungen.
- Die 3 Gleichungen bekommt man durch die Koordinaten von 3 beliebigen Punkten des Graphen.
- Durch geschickte Wahl der 3 Punkte kann man eine Menge Arbeit sparen.
- Wählen Sie t1=0, t2=28 (z.B.) , t3 = 44 (z.B.). (Sie können auch andere Werte wählen!)
- Notieren Sie die 3 Gleichungen, die Sie durch die 3 gewählten Werte(paare) bilden können.
- Das Gleichungssystem aus 3 Glg. mit 3 Parametern A,B,C wird reduziert in ein System aus 2 Glg. mit den beiden Parametern A u. B.
- Die Division der beiden Glg. durcheinander ergibt eine Glg. mit dem einen Parameter B.
- Diese Glg. ist mit der SOLVER-Funktion des Taschenrechners lösbar.
- Geben Sie dazu einen Startwert ein, der zwischen -0,06 und -0,011 liegt. (Was passiert bei anderen Startwerten?)
- oder Sie lassen sich die Lösung berechnen mit www.wolframalpha.com
- oder Sie lösen graphisch mit wzgrapher
- Wenn nun B bekannt ist, lassen sich A und C ebenfalls berechnen.
- Lösung: T(t)= 61,44°C * e-0,02393t + 28,56°C
- Berechnen Sie als Proben die Temperaturwerte bei t1, t2 und t3.
- andere Probemöglichkeit: stellen Sie in Excel den Funktionsgrafen dar.
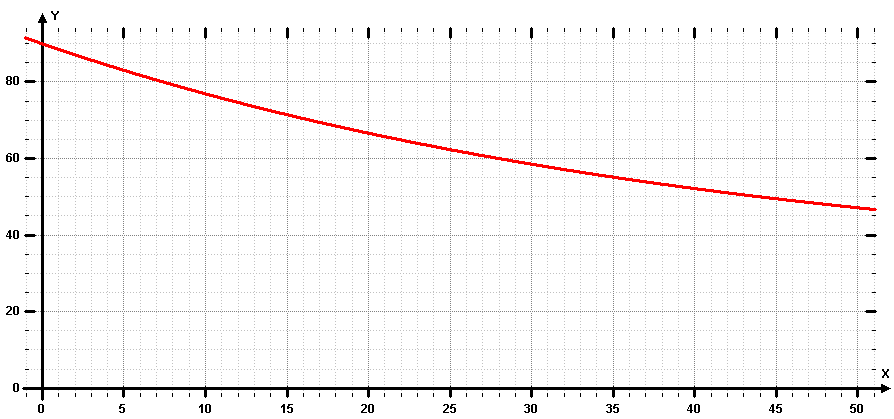
z.B. WZGRAPHER liefert zum Lösungs-Funktionsterm den oben abgebildeten Graph.
Wodurch unterscheiden sich die Temperaturverläufe aus den beiden Aufgaben 17 und 18?
|
|
