Autoelektrik (Startseite)

andere Kfz-Technik

Ladungssicherung

Niederzurren

zuletzt bearbeitet am 18.08.2005

Niederzurren Spanset

Trägheitskräfte

Formelzeichentabelle

Gleitreibwerte-Tabelle

Berechnungsformeln / Tabelle

Beispiele

Links

Beim Niederzurren geht es darum, die Ladung so fest auf die Ladefläche zu pressen, dass allein durch die Reibung die Ladung während der Fahrt nicht verrutscht. Hier wird gezeigt, wie man die erforderliche Zahl von Zurrgurten bestimt.

Seitenanfang

Trägheitskräfte

Formelzeichentabelle

Trägheitskräfte

Formelzeichentabelle

Berechnungsformeln / Tabelle

In den weiter unten aufgeführten Berechnungsformeln / Tabelle und Beispielen werden folgende Formelzeichen genutzt:
Formelzeichen	Bedeutung	Einheit Bemerkung
F	Kraft	N, daN, kN, ...
m	Masse	g, kg, t Eine Ladung von 3,7t (3700kg) Masse hat eine Gewichtskraft von 3700daN
a	Beschleunigung	m/s²
v	Geschwindigkeit	m/s, km/h, ...
r	Kurvenradius	m, km, ...
F_G	Gewichtskraft (der Ladung)	N, daN F_G=m*g (g=10m/s²)
F_T	Trägheitskraft (der Ladung)	daN
F_R	Reibungskraft	daN F_R= μ * F_G
μ	Reibwert	ohne Einheit siehe Tabelle
F_N	Normalkraft	daN normal bedeutet, dass die Kraft im rechten Winkel auf die Ladefläche wirkt. F_N = F_G + F_zg
F_zg	GesamtZurrkraft	daN Kraft, mit der alle Zurrmittel die Ladung zusätzlich zum Eigengewicht auf die Ladefläche drücken. F_zg = z * F_z1
z	Anzahl der Gurte	ohne Einheit Es werden lauter gleiche Gurte verwendet!
F_z1	EinzelZurrkraft	daN Kraft, mit der ein Zurrmittel die Ladung zusätzlich zum Eigengewicht auf die Ladefläche drückt. F_z1 = 2 * F_v * sinα
F_v	Vorspannkraft	daN Zugkraft in einem Gurt. Für F_v ist entweder s_TF (s.Gurtetikett) einzusetzen oder ein durch Messung nachweisbarer tatsächlicher Wert der Gurtspannkraft.
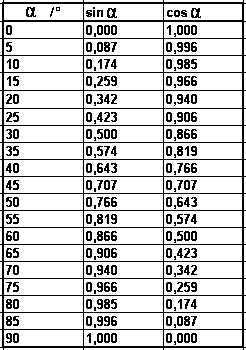
α	Zurrwinkel	° Je näher α bei 90° liegt, desto besser. α darf nicht kleiner als 35° sein! Wer den Sinus-Wert nicht berechnen will, kann ihn ungefähr dieser Tabelle entnehmen.

Gleitreibwerte Tabelle

Der Reibwert wird immer für eine Materialpaarung angegeben: 2 Materialien reiben aufeinander. Die Tabelle zeigt die sehr unterschiedlichen Werte abhängig von der Materialpaarung und von Umgebebungsbedingungen (trocken, nass, fettig).

Der Reibwert μ=0,2 bedeutet, dass man F_R=200daN Kraft aufwenden muss, um eine Ladung der Masse m=100kg bei diesem Reibwert auf der Ladefläche zu verschieben (F_R = μ * F_G).

Bei der Ladungssicherung wird nicht der Haftreibwert sondern der Gleitreibwert genutzt, um die Fahrzeugvibrationen zu berücksichtigen.

Ist der Gleitreibwert unbekannt, muss man μ = 0,2 in die Formel einsetzen.

Bei der Verwendung von Antirutschmatten beträgt μ = 0,6.
Antirutschmatta

Antirutschmatta

Formelzeichentabelle

Berechnungsformeln / Tabelle

Beispiele

Bei der Berechnung zum Niederzurren muss die Anzahl der erforderlichen Zurrgurte bestimmt werden, wenn alle anderen Daten bekannt sind.
Dazu stellen Sie sich eine Ladeplattform vor ohne Bordwände, ohne Rungen oder sonstigen möglichen Formschluss. Die Ladung wird also auf der Ladefläche abgestellt und nur durch ihr Eigengewicht und die Zurrmittel gesichert.

1.	Niederzurren als Ladungsicherung ist ein reiner Kraftschluss oder Reibschluss, weil ausschließlich die Reibung zwischen Ladung und Ladefläche ein Verrutschen der Ladung verhindert. Damit das auch der Fall ist, muss gelten, dass die Reibungskraft größer (oder mindestens gleich) der Trägheitskraft ist, die die Ladung verschieben will. Um etwas einfacher rechnen zu können verzichte ich jetzt auf das > -Zeichen und rechne nur noch mit echten Gleichungen. Zu beachten ist dann jedoch Folgendes: Sollte auf diese Weise berechnet werden, dass z.B. 4,13 Gurte erforderlich sind, eine bestimmte Ladung zu sichern, so muss dieses Ergebnis natürlich immer aufgerundet werden (also 5 Gurte), um auf der sicheren Seite zu sein.	Reibungskraft >= Trägheitskraft	F_R >= F_T
2.	Die Reibungskraft F_R hängt von der Kraft ab, mit der die Ladung gegen die Ladefläche gepresst F_N (Normalkraft) wird und von der Reibungszahl μ. Die Reibungszahlen bzw. Reibbeiwerte oder Reibungskoeffizienten μ für die unterschiedlichen Reibsituationen wurden experimentell ermittelt und können einer Tabelle entnommen werden.	Reibungskraft = Normalkraft * Reibbeiwert	F_R = F_N * μ
3.	Die Trägheitskraft F_T wurde weiter oben bereits erklärt. Da die größten Trägheitskräfte beim Bremsen auftreten, reicht es beim Niederzurren für diesen Fall die Ladung zu sichern. Wenn die Ladung bei einer Vollbremsung nicht rutscht, dann tut sie es bei der Beschleunigung oder Kurvenfahrt erst recht nicht.	Trägheitskraft = 0,8 * Gewichtskraft	F_T = 0,8 * F_G
4.	Setzt man nun in die erste Gleichung die Formeln für die Trägheitskraft und die Reibungskraft ein, so ergibt sich:		F_N * μ = 0,8 * F_G
5.	Die Nornmalkraft F_N wird gebildet aus dem Ladungsgewicht und der Kraft, mit der alle Zurrgurte die Ladung zusätzlich auf die Ladefläche pressen:	Normalkraft = Ladungsgewicht + Gesamtzurrkraft	F_N = F_G +F_zg
6.	Wenn man Gleichung 5 in Gleichung 4 einsetzt, ergibt sich:	(Ladungsgewicht + Gesamtzurrkraft) * Reibwert = 0,8 * Ladungsgewicht	(F_G+F_zg) * μ = 0,8 * F_G
7.	Wenn man Gleichung 6 durch μ dividiert, ergibt sich:	Ladungsgewicht + Gesamtzurrkraft = 0,8 * Ladungsgewicht / Reibwert	F_G +F_zg = 0,8 * F_G / μ
8.	Wenn man von der Gleichung 7 F_G subtrahiert, ergibt sich:	Gesamtzurrkraft = 0,8 * Ladungsgewicht / Reibwert - Ladungsgewicht	F_zg = 0,8 * F_G / μ - F_G
9.	Die gesamte Zurrkraft ergibt sich indem man die Einzelzurrkraft mit der Gurtzahl z multipliziert (lauter gleiche Zurrgurte):	Gesamtzurrkraft = Gurtanzahl * Einzelzurrkraft	F_zg = z * F_z1
10.	Einsetzen in Gleichung 8 führt zu:		z * F_z1 = 0,8 * F_G / μ - F_G
11.	Wenn Gleichung 10 durch F_z1 dividiert wird, erhält man: Hier hat man endlich eine Formel für die erforderliche Gurtzahl z, jedoch ist F_z1 noch unbekannt.		z = (0,8 * F_G / μ - F_G) / F_z1
12.	Die Abbildung zeigt die Vorspannkraft F_G und den Zurrwinkel μ. Wenn der Zurrwinkel μ 90° beträgt, so zerrt ein Gurt die Ladung mit genau der 1,5-fachen Vorspannkraft auf die Ladefläche. Wenn der Zurrwinkel < 90° ist, kann man mit dem rechtwinkligen Dreieck A-B-C (Formelsammlung) die senkrecht wirkende Komponente der Vorspannkraft berechnen. Auch wenn Kantenschutzwinkel/ Kantengleitwinkel (s. untere Abb.) genutzt werden, so setzt man auf der Spannschlossseite die volle Vorspannkraft ein aber vorsichtigerweise auf der gegenüberliegenden Seite nur die halbe Vorspannkraft. Man geht davon aus, dass ein Teil der Zurrkraft in den Umlenkpukten verloren geht.		F_z1 = 1,5 * F_v * sinα
13.	Dies wird nun in Gleichung 11 für F_z1 eingesetzt und ergibt:		z = (0,8 * F_G / μ - F_G) / (1,5 * F_v * sinα) oder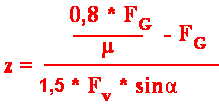
Für F_v darf man nur den Wert einsetzen, der auf dem Gurtetikett mit s_tf (Standard Tension Force) bezeichnet ist, auch wenn die maximale Zugkraft (LC = Lashing Capacity) viel größer ist! Bei dem abgebildeten Gurt beträgt s_tf 500daN und LC 2500daN!
Wenn man allerdings die tatsächliche Vorspannkraft im Gurt gemessen hat, dann darf man auch diese (meist höhere) Kraft einsetzen und wird dafür mit weniger Arbeit beim Gurten belohnt. Ein Gurt darf höchstens bis zur halben LC gespannt werden! Der Grund dafür liegt in dynamischen Zusatzbelastungen des Gurts während der Fahrt, wodurch der Gurt sonst überlastet werden könnte und reißt

Tabelle Einfachmethode Niederzurren

Berechnungsformeln / Tabelle

Beispiele

Links

1. Beispiel	2. Beispiel
Gegeben: Masse der Ladung m = 12,7t Zurrwinkel α = 65° Gleitreibwert unbekannt : also μ= 0,2 !! Vorspannkraft (nicht gemessen) : also F_v = s_TF = 500daN	Gegeben: Masse der Ladung m = 12,7t Zurrwinkel α = 85° Gleitreibwert Antirutschmatte : also μ= 0,6 !! Vorspannkraft (gemessen) : also F_V = 750daN
Gesucht: erforderliche Gurtzahl z	Gesucht: erforderliche Gurtzahl z
Lösung: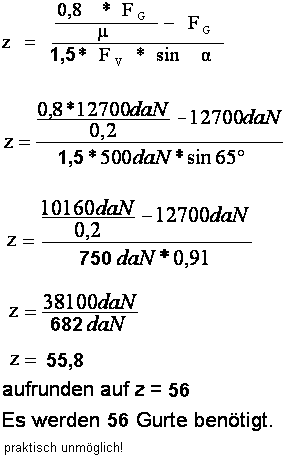	Lösung: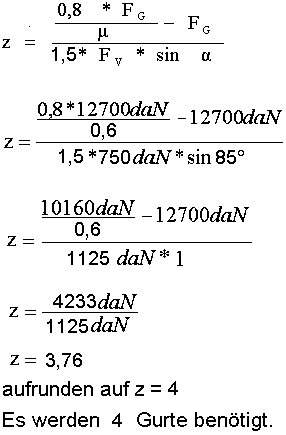

Der Vergleich der beiden Aufgaben zeigt die Bedeutung

des Zurrwinkels α
des Gleitreibwerte μ

Beispiele

Links

Seitenende

Gurtzahlberechnung mit Excel-Tabelle

Javascript Niederzurren -->Daten in eine Maske eingeben --> Schalter betätigen --> Gurtzahl wird berechnet und angezeigt

Die Hersteller von Ladungssicherungsmaterialien Dolezych und Spanset bieten auf ihren Sites Informationesmaterial, insbesondere wenn man in die Verkaufskataloge schaut (download).

Seite:

174