Seitenende Autoelektrik (Startseite)

Grundlagen der Elektrotechnik


Wechselstrom, Grundlagen




zuletzt bearbeitet am 11. 2. 2003 		Wechselspannung

Wechselspanungs-generator


Begriffe zur Wechselspanung


Effektivwert



















Wie ist ein Wechslespannungsgenerator im Prinzip aufgebaut?

Welche Eigenschaften hat die Wechselspannung / der Wechselstrom?

Einige Berechnungsbeispiele zu Frequenz, Periode, Scheitelwert und Augenblickswert





Seitenanfang

Wechselspanungsgenerator

Begriffe zur Wechselspanung










Wechselspannungen spielen als Energieträger im Kfz keine Rolle. Sie entstehen jedoch in Induktivgebern und werden außerdem zunächst als Drehspannung im Kfz-Generator erzeugt, bevor diese gleichgerichtet und geregelt ins Bordnetz eingespeist wird.
Dieses Kapitel soll für ein leichteres Verständnis für diese beiden Kfz-typischen Wechselstromanwendungen sorgen.




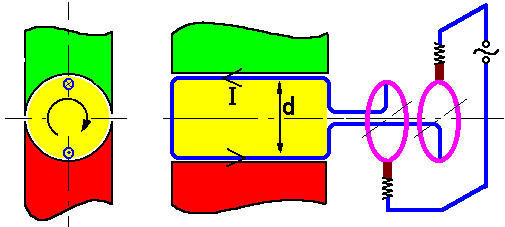Wechslespannungsgenerator Ein Wechselspannungsgenerator besteht im Prinzip aus den Bauteilen


In der Prinzipskizze erkennt man den Rotor (gelb), die Rotorwicklung (blau), die Schleifringe (lila) und die Kohlebürsten (braun)
Anstelle eines Stators aus Eisenkern und Statorwicklung hat dieser Generator einen Permanentmagnet als Stator.

Wird nun der Rotor z.B. über eine Riemenscheibe mit konstanter Drehzahl angetrieben, so wird in der Rotorwicklung eine Spannung induziert
(siehe dazu Lorentz-Kraft oder Induktion)


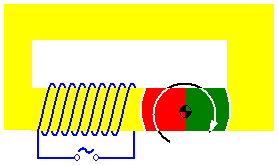Wechslespannungsgenerator ohne Schleifringe Vielleicht ist dir schon aufgefallen, dass ein solcher Generator eine Fehlkonstruktion ist (obwohl er zweifellos gut funktioniert). Denn der selbe Effekt lässt sich mit einer wesentlich weniger aufwändig gebauten Maschine erreichen, wenn man als Rotor einen Permanentmagneten wählt und die induzierte Spannung an der Ständerwicklung abgreift. Auf diese Weise spart man die Schleifringe und Kohlebürsten und hat somit außer den Lagern keine Verschleißteile mehr im Generator. Der Fahrraddynamo ist ein typischer Vertreter dieser Generatorenklasse.
Wie Drehstrom erzeugt wird, erfährt man unter Drehstromgenerator







Wechselspanungsgenerator

Begriffe zur Wechselspanung

Effektivwert










Mit der Rotorstellung während einer Umdrehung ändert sich ständig die Spannung an den Generatorklemmen. Eine gleichmäßige Drehbewegung erzeugt eine sinusförmige Spannung, wobei bei jeder Umdrehung exakt eine volle Spannungsschwingung entsteht. Dabei pendelt die Spannung von 0V über den positiven Scheitelwert (Us), wieder abnehmend durch Null in den negativen Spannungsbereich, dort durch den negativen Spannungsscheitelwert (-Us) zurück zu 0 Volt. Bei der nächsten Umdrehung wiederholt sich dieses Spiel. 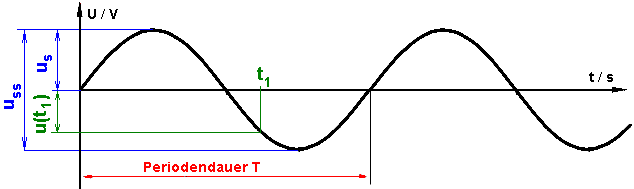Wechselspannungsdiagramm So entsteht eine periodische Spannungslinie, die ständig zwischen den Scheitelspannungen (=Spitzenspannungen) hin und herpendelt. Wie bei allen periodischen (zeitlich stets wiederkehrend) Vorgängen kann man genaue Voraussagen machen, sobald man eine Periode genau kennt.
Der Ausdruch u(t) bedeutet, dass die Spannung u eine von der Zeit t abhängige Größe ist. U ist eine Funktion der Zeit. u(t1) ist die Augenblicksspannung zum Zeitpunkt t1. Eine volle Periode später, ist die Spannung wieder genau so groß und so ist es für alle Zeiten, die eine beliebige ganze Zahl von Periodendauern von t1 entfernt sind (früher oder später, egal).
Dem Kurvenverlauf ist außerdem zu entnehmen, dass zum Zeitpunkt t2 die Spannung den selben Wert hat wie zum Zeitpunkt t1 (wenn auch mit anderer Steigung), und man entnimmt dem Diagramm, dass wegen Symmetrie die Zeiten t3 und t4 gleich lang sind.

All diese Eigenschaften lassen sich mit folgenden Formeln exakt beschreiben und dienen zur Berechnung dieser Sinuslinien:

Formeln zur Sinusfunktion / Wechslespannung / Wechslestrom
FormelErläuterung
u(t)= u( t + Z * T )Periodizität der Sinusfunktion.
Die Spannung zur Zeit t ist genau so groß wie die einige (Z = ganze Zahl) Perioden (T) später bzw. früher. Probieren sie es mit dem Taschenrechner aus sin (35°) = sin (35° + 10 * 360°). (360° ist die Periode des Sinus)
u(t) = -u(-t)Rotationssymmetrie zum Nullpunkt.
Probieren sie es mit dem Taschenrechner aus sin (35°) = - sin (-35°).
u(t) = Us * sin( α)Den Augenblickswert der Spannung kann man berechnen, wenn man den Scheitelwert (Us) und den Drehwinkel (α) kennt.
z.B. u(348°) = 318V * sin(348°) = -66,11V, wenn die Scheitelspannung 318V beträgt.
ω = 2* π * fDie Kreisfrequenz (ω) wird nach der links stehenden Formel berechnet, wobei f die Frequenz der Wechselspannung ist.
z.B. ergibt sich für f = 50Hz (= 50/s) : ω= 2* π * 50/s = 314,159/s.
Diese Berechnung wird gleich benötigt.
α = ω * tDen Drehwinkel (α) kann man berechnen, wenn man die Winkelgeschwindigkeit (=Kreisfrequenz) (ω) und die Zeit (t) kennt.
z.B. mit ω=100/s und t = 20ms (=0,02s) ergibt sich ein Drehwinkel von: α = 100/s * 0,02s = 2 !!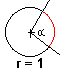
Bogenmaß Diese Winkelangabe ist ungewöhnlich, da sie nicht in der Einheit ° erfolgt, sondern im Bogenmaß. Dieser ist die Bogenlänge auf einem Kreis mit dem Radius 1 und dem üblichen Winkel α in °. 360° entspricht also im Bogenmaß dem vollen Umfang dieses Einheitskreises (mit r = 1) von 6,28.
Erforderliche Umrechnungen können sie nun z.B. per Dreisatz vornehmen mit dem Eingangssatz 360° = 6,28(=2*π)
Um den Sinus eines Winkels im Bogenmaß mit dem Taschenrechner berechnen zu können, müssen sie diesen erst in den Modus Bogenmaß umschalten (siehe hierzu die Bedienungsanweisung des Taschenrechners). Meist wird dies im Display des Taschenrechners mit rad angezeigt, denn rad ist die Einheit des Winkels im Bogenmaß, so wie °die Einheit des Winkels im Gradmaß ist.
φDen Startwinkel φ muss man im Argument des Sinus noch addieren, falls der Rotor zum Zeitpunkt 0 nicht den Winkel 0 hat.
Damit lautet die vollständige und allgemeingültige Formel :u(t)=Us * sin (ω, * t + φ)
u(t)=Us * sin (2 * π *f * t + φ)So lautet schließlich die vollständige und allgemeingültige Formel zur Berechnung der Augenblicksspannung für beliebige
  • Scheitelspannungen Us
  • Frequenzen f
  • Zeiten t
  • Startwinkel φ .
f = 1 / TDie Frequenz ist der Kehrwert der Periodendauer (und umgekehrt).













































Hier nun ein paar Beispielaufgaben:
Gegebene Größengesuchte GrößenLösungen
α= 2878°
Us= 273V		u(α)u(α)=Us*sinα= 273V*sin 2878°=273V* (-0,0349)= -9,528V
Manche Taschenrechner mögen keine Winkel >360°!. Dann muss man sich entweder einen anderen Taschenrechner kaufen oder die Periodizität der Sinusfunktion ausnutzen. Dazu ermittelt man, welcher Restwinkel übrigbleibt, wenn man alle vollständigen 360° Perioden von 2878° subtrahiert.
Hier wäre also zu berechnen: 2878°/360°= 7,99444.
Das heißt es gibt 7 ganze + 0,99444 360° Perioden.
0,99444 * 360°= 358°.
Also gilt sin (2878°)=sin(7*360°+358°)= sin 358°=-0,0349
Us= 14,8V
u(α)=3,6V		αu(α)=Us*sin α
diese Formel nach sin α umstellen ergibt:
sin α= u(α) / Us. Es ist aber nicht sin α gesucht, sondern α. Daher ist noch die Umkehrfunktion vom Sinus anzuwenden (auf dem Taschenrechner meist mit sin-1 angegeben).
α= sin-1 (u(α) / Us.) = sin-1( 3,6V / 14,8V) = sin-1( 0,243) = 14,08°.
α= -287°
u(α)=17V		Usu(α)=Us*sin α
diese Formel nach sin Us umstellen ergibt:
Us =u(α)/sin α= 17V /sin(-287°) = 17V / 0,956 = 17,78V
ω=2,87/s,
t = 5,6min		αα =ω * t = 2,87/s, * 5,6min = 2,87/s, * 336s = 964,32rad = 55251,47° = 153,48 * 360° = 153 volle Umdrehungen + 171,47°
zur Erinnerung: 6,28318... rad = 360°. Dabei ist rad die Winkeleinheit im Bogenmaß
f= 60Hz,
α = 145° 		ω,
t		ω=2 * π * f = 2 * π * 60/s = 377/s = 377rad/s = 60 * 360°/s = 21600°/s
α = ω *t => t = α / ω = 145° / (21600°/s)= 6,713ms oder t = α / ω = 145° / (377/s)= 2,53rad / (377/s)=6,713ms
(Entweder sie arbeiten im Gradmodus oder sie setzen die Winkelgeschwindigkeit in rad/s und den Winkel in rad ein.)
f = 30Hz, t=1,25 Us= 27Vu(t)u(t) = Us * sin(ω * t) = Us * sin(2 * π * f * t) = 27V * sin(2 * π * 30Hz * 1,25s) = 27V * sin(235,619) = 27V * (-0,8253) = -22,28V
Hinweis: Taschenrechner im Bogenmaßmodus!




































Begriffe zur Wechselspanung

Effektivwert

Seitenende







Baut man einen einfachen Stromkreis, der aus einer Wechselspannungsquelle und einem Widerstand besteht und misst die Spannung am Widerstand mit einem Oszilloskop und gleichzeitig mit einem Digitalmultimeter, so zeigen beide Messgeräte verschiedene Werte an!


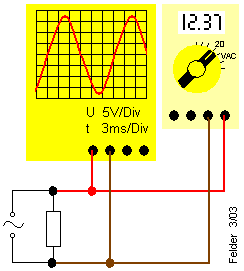
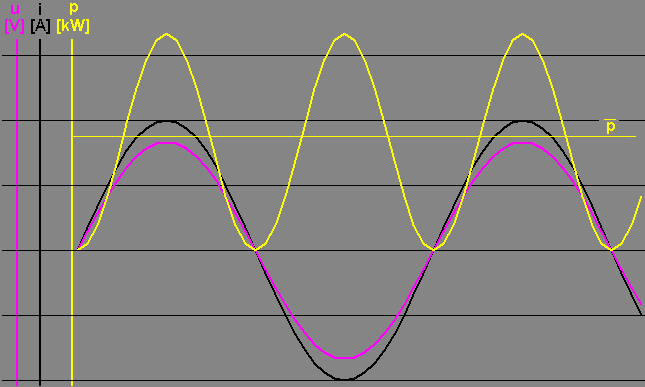
Scheitelwert-Effektivweret




Beim Oszilloskop ist die Sache klar : Es wurde der Scheitelwert der Spannung us abgelesen (3,5Div) und mit dem eingestellten Skalierungsfaktor (5V/Div) multipliziert.

Was aber zeigt das Digitalmultimeter an?
Übrigens würde ein Analogmessgerät auch 12,37V anzeigen.


Scheitelwert-Effektivweret
Schauen sie sich dazu die drei im nebenstehenden Diagramm gezeigten Kurven an. Sie geben jeweils den zeitlichen Verlauf von Spannung, Strom und Leistung des Widerstands an.

Bei rein ohm´schen Widerständen gelten die selben Gesetze wie im Gleichstromkreis. Komplizierter (und interessanter) wird es, wenn auch andere Elemente (Kondensatoren oder/ und Spulen) im Wechselstromkreis eingebaut sind.

Insbesondere gilt hier auch das ohm´sche Gesetz und das P=U*I ist. Zu beachten ist jedoch, dass sich die Werte mit der Zeit ständig ändern. So ist natürlich der Strom durch den Widerstand 0A, wenn die Spannung gerade 0V beträgt. Auch ist zu diesen Zeitpunkten die Leistung am Widerstand =0W.

Stellen sie sich einen Heizwiderstand (Tauchsieder) vor, mit dem sie Wasser für eine Tasse Kaffe erwärmen wollen.

Da Spannung und Strom gleichzeitig ihre Richtung ändern, da also entweder Strom und Spannung entweder beide gleichzeitig positiv oder beide negativ sind, ist jeder Augenblickswert der Leistung immer nur positiv (minus mal minus gibt plus).

Um deutlich zu machen, dass Spannung, Strom und Leistung zeitlich veränderliche Größen sind, benutzt man kleine Formelzeichen, also u, i und p.

Aus der Symmetrie der Kurvenzüge sind die zeitlichen Mittelwerte eindeutig bestimmbar und es ergibt sich:


Peff = U2eff / R
Um die Antwort (Was zeigt das DMM an?) zu finden, sind nun einige Berechnungen erforderlich:
1p(t) = u(t) * i(t)Der Augenblickswert der Leistung am Widerstand ergibt sich aus dem Produkt von Augenblickswert der Sapnnung und Augenblickswert des Stroms.
2Pmax = Umax* ImaxDie Maximalleistung am Widerstand hat man zu dem Zeitpunkt, wenn die Spannung am Widerstand maximal ist. Dann ist glücklichwerweise auch der Strom durch den Widerstand maximal.Peff Das gilt nicht mehr, sobald Induktivitäten oder Kapazitäten im Wechselstromkreis sind!
3Imax = Umax / RDas ohm´sche Gesetz gilt weiterhin.
4Pmax = U2max / RImax wurde in die Pmax-Gleichung eingesetzt.
5Pmittel = Pmax /2Der Durchschnittswert der Leistung ist halb so groß wie der Maximalwert der Leistung.
6Pmittel = U2max / (R * 2)Es wurde das Ergebnis von Gleichung 4 in Gleichung 5 eingesetzt.
7Pmittel = Peff = PPeff ist die effektive Leistung am Widerstand mit der das Kaffeewasser erhitzt wird.
Statt effektiver Leistung oder mittlerer Leistung wird einfach Leistung gesagt.
8Peff = Ueff * IeffDamit werden die beiden neuen Begriffe Ueff Effektivspannung und Ieff Effektivstrom eingeführt.
9Ieff = Ueff / RAuch hierfür gilt selbstverständlich das ohm´sche Gesetz.
10ergibt sich aus den Gleichungen 8 und 9
11U2eff / R = U2max / (R * 2)ergibt sich aus den Gleichungen 6 und 10
12U2eff = U2max / 2ergibt sich , wenn Gleichung 11 mit R multipliziert wird
13Ueff = Umax / Wurzel(2)ergibt sich , wenn aus Gleichung 12 die Quadratwurzel gezogen wird
14

Ueff = Umax / 1,414

Nun haben sie´s geschafft!!

Der Scheitelwert einer Wechselspannung ist 1,414 mal so groß wie der Effektivwert derselben Wechselspannung

Rechnen Sie doch einmal die Messwerte aus dem Versuch oben nach!

Am Oszilloskop ist der Scheitelwert einer Wechselspannung ablesbar, ein Multimeter zeigt dagegen den Effektivwert an.

Bei den meisten Multimetern gilt dies jedoch nur bei sinusförmigen Wechselspannungen! Sogenannte TRUE RMS - DMM zeigen dagegen auch für beliebeig geformte Wechselspannungen den Effektivwert an.
Statt Ueff sagt man auch einfach nur U.

Eine Wechselspannung mit einem Effektivwert von U = 14V hat an einem Heizwiderstand dieselbe Wirkung wie eine Gleichspannung von 14V.






























Seitenanfang Quickstart eMail an Autor Startseite zurückblättern vorblättern Stichwortverzeichnis Aufgaben Seite:

33