
Musterlösungen, Übersicht und Links
Musterlösungen

Berufskolleg Mitte - Essen


|
Autoelektrik ( Startseite) Musterlösungen, Übersicht und LinksMusterlösungen |
 Berufskolleg Mitte - Essen |

|
| vorige Seite | 2.01 Gebrochenrationale Funktionen |
nächste Seite |
1. Aufgabe |
2. Aufgabe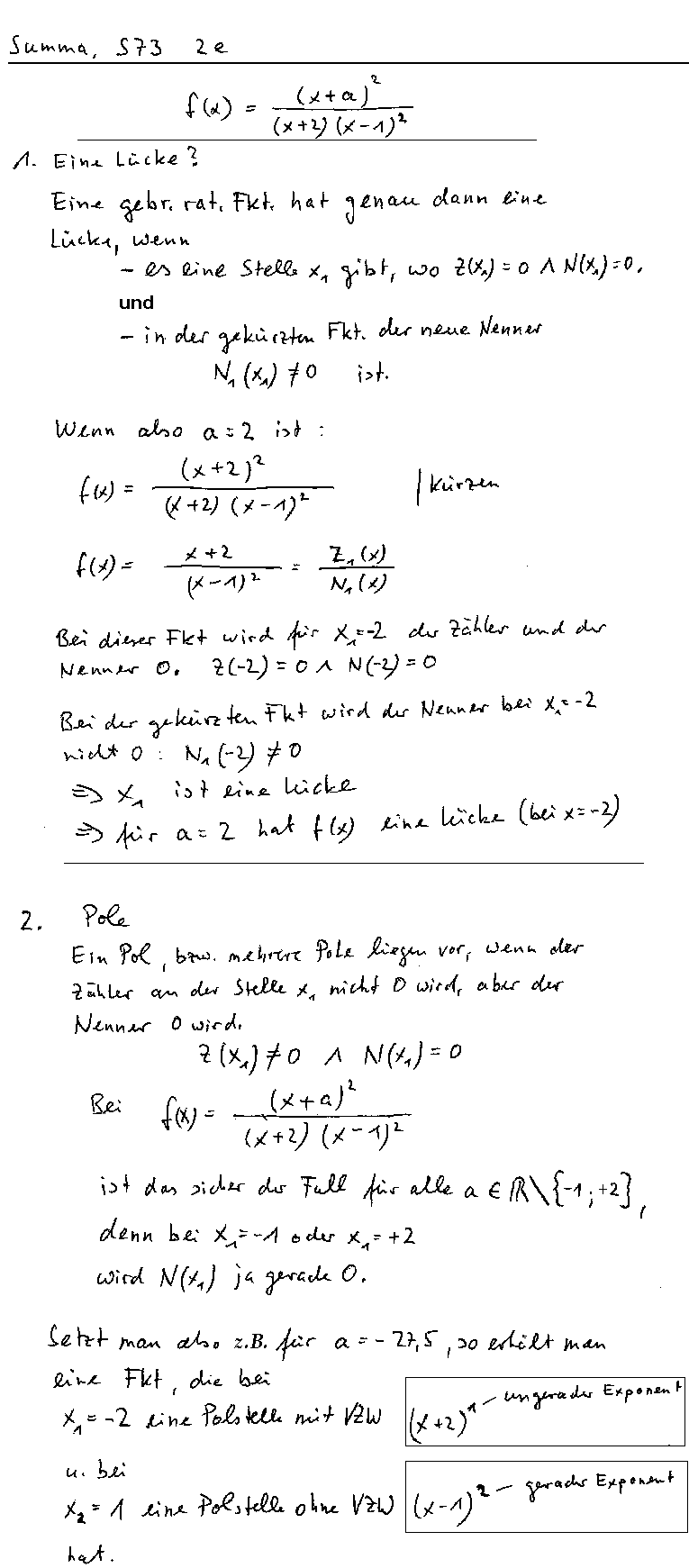 |
3. Aufgabe |
4. Aufgabe |
5. Aufgabe |
6. Aufgabe |
7. Aufgabe |
8. Aufgabe |
9. Aufgabe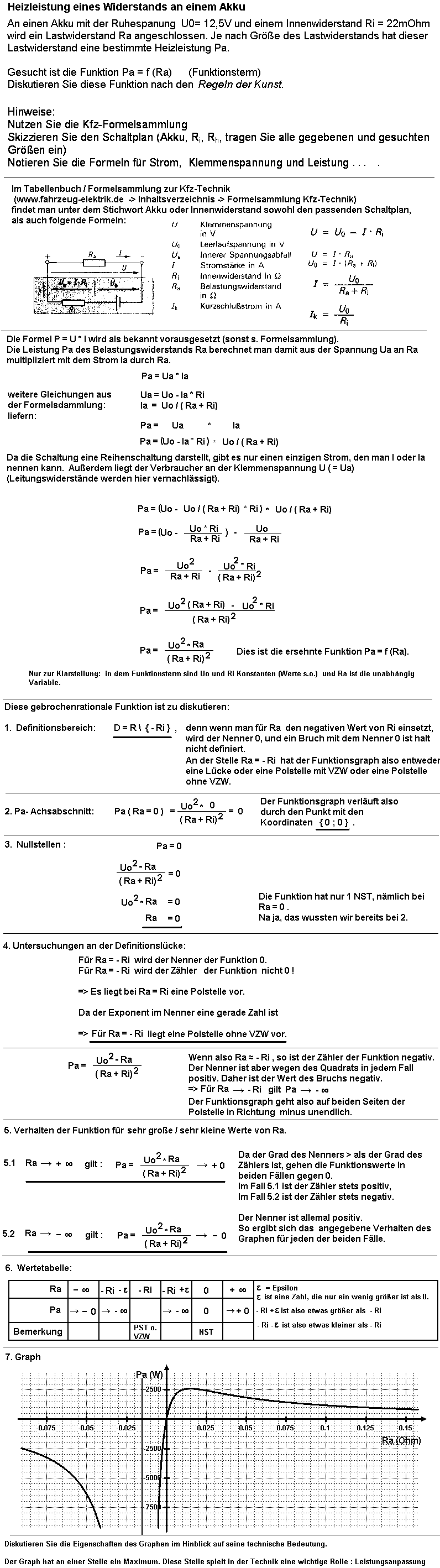 |
10. Aufgabe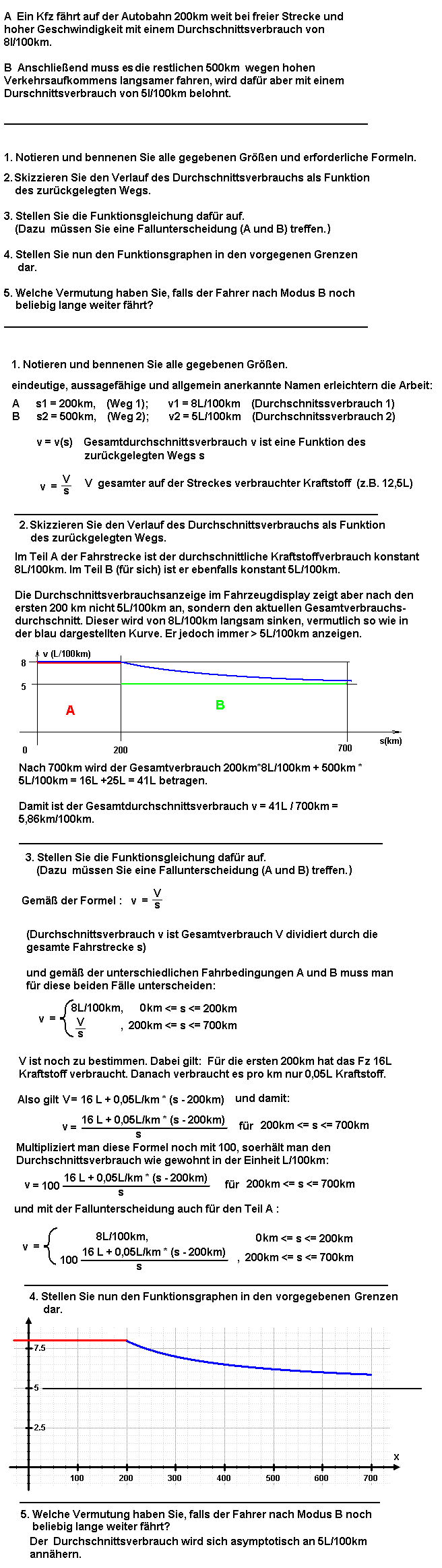 |
11. Aufgabe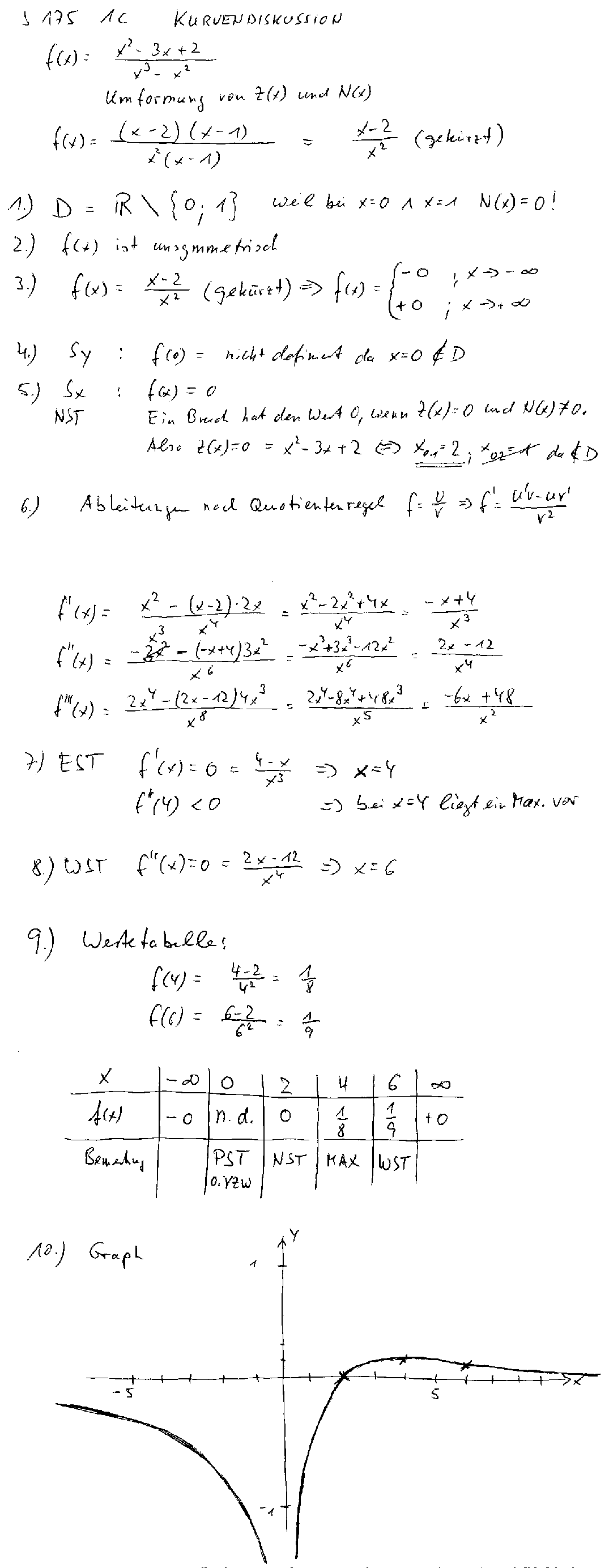 |
12. Aufgabe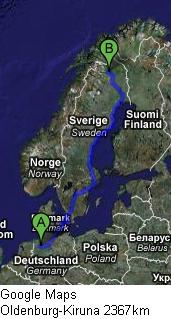 Moderne Fahrzeuge haben einen Bordrechner. Neben vielen anderen Funktionen berechnet der auch die Durchschnittsgeschwindigkeit
vm (mittlere Geschwindigkeit) einer Fahrt z.B. von Oldenburg (Kreis Oldenburg) nach Kiruna (Nordschweden).
Er zeigt darüberhinaus sogar den aktuellen Wert an, der bisher bei dieser Reise erzielt wurde. Aktualisiert wird dabei nicht kontinuierlich,
sondern z.B. alle 15s.
Moderne Fahrzeuge haben einen Bordrechner. Neben vielen anderen Funktionen berechnet der auch die Durchschnittsgeschwindigkeit
vm (mittlere Geschwindigkeit) einer Fahrt z.B. von Oldenburg (Kreis Oldenburg) nach Kiruna (Nordschweden).
Er zeigt darüberhinaus sogar den aktuellen Wert an, der bisher bei dieser Reise erzielt wurde. Aktualisiert wird dabei nicht kontinuierlich,
sondern z.B. alle 15s.Man kann sich vorstellen, dass zu Beginn einer Fahrt (im Stadtgebiet von Flensburg) diese Durchschnittsgeschwindigkeit sich relativ häufig und relativ stark ändert, auch noch, sobald man die Stadt verlassen hat und bei freier Fahrt zügig unterwegs ist. Die Anzeige zu beobachten wird jedoch mit zunehmender Fahrtdauer immer uninteressanter, weil sich immer weniger verändert, je länger man unterwegs ist. Woran liegt das denn eigentlich? Nun zur eigentlichen Aufgabe: Auf dieser beschriebenen Reise (sie dauert vermutlich länger als 30 Stunden) fuhr das Fahrzeug die ersten 5 1/4 Stunden zwar mit häufig unterschiedlicher Geschwindigkeit, im Durchschnitt jedoch mit 100km/h. In Malmö (Schweden) dann stellte der Fahrer den Tempomat auf die erlaubten 80km/h ein und cruiste auf diese Weie völlig entspannt die restlichen 1840 km über die gut ausgebauten Landstraßen der wald- und seenreichen Landschaft. So weit so gut. Unmittelbar hinter der schwedischen Grenze stellte der Fahrer das Display des Bordrechners so ein, dass gerade die Gesamtdurchschnittsgeschwindigkeit der Gesamtreise angezeigt wurde, beobachtete wie diese sich allmählich veränderte und grübelte über die Funktion nach, mit der man das zeitliche Verhalten dieser Anzeige beschreiben konnte. So hielt er sich zwar bis Kiruna wach, konnte die Lösung jedoch nicht finden. Schaffen Sie´s? LösungAus den in der Aufgabe enthaltenen Angaben kann man zunächst berechnen, dass in den ersten 5 1/4 Stunden eine Strecke von 525km (Oldenburg-Malmö) zurückgelegt wurden und dass für die restlichen 1840km eine Zeit von 23 Stunden benötigt wurden. Insgesamt war die Strecke also 2365km weit und wurde in 28,25 Stunden zurückgelegt. Nun zur Durchschnittsgeschwindigkeit:In Malmö angekommen zeigte das Display genau vm = 100km/h an.Da war das Fahrzeug bereits 525km und 5,25 Stunden unterwegs. In Kiruna angekommen muss das Display genau vm = 83,72km/h angezeigt haben. Denn da war das Fahrzeug 2365km und 28,25 Stunden unterwegs. Während der Fahrt durch Schweden muss sich der Wert von vm also kontinuierlich von 100km/h auf 83,72km/h verringert haben. So weit kann noch jeder diese Überlegungen und Berechnungen durchführen. Nun zur Funktion:Zunächst einmal ein paar Vorüberlegungen:
Mit der Formel muss man einfach weiter experimentieren: Von Malmö an läuft also t. Dort ist aber s bereits 525 km und vm=100km/h bereits im Bordrechner gespeichert! Wenn nun jede Stunde 80km zur Strecke dazukommen, so ist vm nach einer Fahrstunde in Schweden 605km/6,25h = 96,8km/h. Konkret wurde also so gerechnet: vm = (525km +80km)/ (5,25h + 1h) Nach diesem Verfahren könnte man stundenweise weiterrechnen und erhielte so folgende Wertetabelle:
Da nun schon so fleißig mit konkreten Werten die Durchschnittsgeschwindigkeiten zu verschiedenen Zeiten berechnet wurden, kann man den Funktionsterm einfach dadurch erhalten, indem man eine konkrete Rechnung verallgemeinert,d.h. nicht die konkreten Zahlenwerte für s und t einsetzt, sondern statt dessen die Variablen s und t : vm = s / t = (525km + s)/(5,25h +t) , wobei hier s der in Schweden zurückgelegte Weg ist und t die in Schweden aufgewendete Fahrzeit. 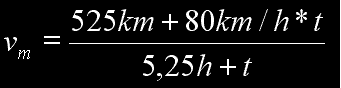 In Schweden gilt aber s = 80km/h * t , einsetzen in die Formel für vm ergibt den gesuchten Funktionsterm:
In Schweden gilt aber s = 80km/h * t , einsetzen in die Formel für vm ergibt den gesuchten Funktionsterm:Dies ist eine gebrochen rationale Funktion! (Deshalb steht diese Aufgabe auch in diesem Kapitel.) Wie man diese Funktionen analysiert, haben Sie in vielen Beispielen oben bereits vorgeführt bekommen. Tun Sie es hier mal selbstständig. 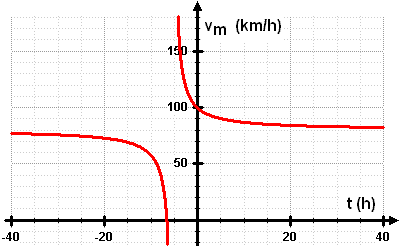 Klar ist, dass
Klar ist, dass |
Funktion und Asymptote | |
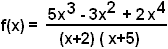
|
Gegeben ist die Funktion mit dem links abgebildeten Funktionsterm. Für welche Werte von x beträgt die relative Abweichung der Werte der Asymptote dieser Funktion und den Werten der Originalfunktion höchstens 1 Promille? |
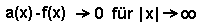
|
Eine Asymptote a(x) ist eine ganzrationale Funktion, deren Funktionswerte um so besser mit denen der Originalfunktion
f(x) übereinstimmen, je weiter die x-Werte von den Definitionslücken entfernt sind. Ist man nur weit genug von den Definitionslücken des Koordinatensystems entfernt, kann die Differenz zwischen Funktionswert und Asymptotenwert beliebig klein werden, insbesondere also auch kleiner als ein Promille (= 1/1000 = 0,001). |
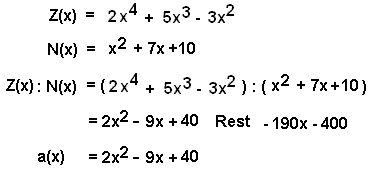
|
Die Asymptotenfunktion erhält man durch algebraische Division des Zählers von f(x) durch den Nenner von f(x),
wobei der Rest keine Rolle spielt. Hier erkennt man auch, dass der Grad von a(x) gleich dem Grad von Z(x) - Grad von N(x) beträgt. Hier: Grad von a(x) = 2. a(x) ist also in diesem Fall eine Parabel. |
|
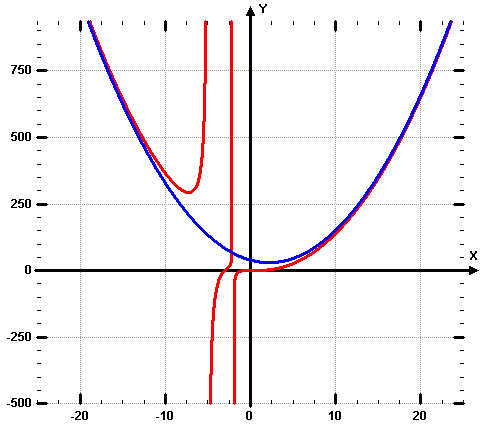
Die Darstellung zeigt die beiden Graphen f(x) und a(x)
Für x < -10 stimmen a(x) und f(x) etwa überein. Für -10 < x < 5 verhält sich f(x) ganz anders als a(x). Für x > 5 stimmen a(x) und f(x) etwa überein. |
|
Die Aufgabe ist nun herauszufinden, für welche Werte von x die relative Abweichung zwischen f(x) und a(x) kleiner als 0,001 ist.
Unter der relativen Abweichung versteht man den Quotienten: Differenz der beiden Werte dividiert durch Funktionswert. Der Graphik kann man bereits ungefähr entnehmen, dass x1 < -10 sein muss und x2 > 5. Außerdem muss es noch 2 weitrere Stellen geben in der Umgebung des Schnittpunkts der beiden Graphen (Funktion und Asymptote). | |
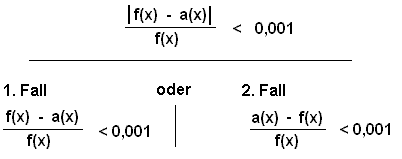
|
Die mathematische Formulierung lautet also: Von vorne herein ist ja nicht klar, ob sich die Funktion von oben oder von unten an die Asymptote anschmiegt, daher die Betragszeichen. Die Betragszeichen lassen sich durch die Fallunterscheidung ersetzen. |
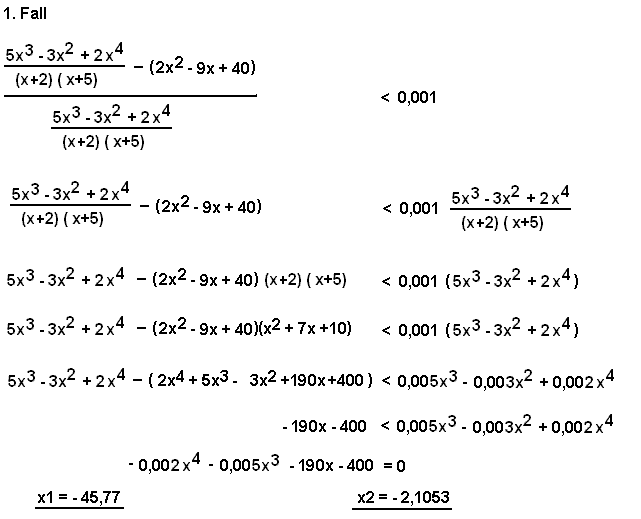
|
Funktionsterme eingesetzt, ergibt sich: Die Gleichung mit dem Nenner multiplizieren: und noch einmal mit dem neuen Nenner multiplizieren: ergibt nach einigen weiteren Umformungen die Gleichung 4. Grades: Das "<" Zeichen wurde durch "=" ersetzt, da diese Gleichung ein TR lösen kann. Jedoch muss man sich nun Gedanken machen, für welche Werte von x das "<" Zeichen gilt. Ein Taschenrechner mit SOLVER-Funktion liefert dazu die beiden Lösungen x1 und x2: |
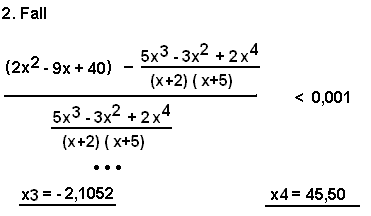
| Der 2. Fall wird analog zum 1. gelöst und ergibt die Lösungen x3 und x4. |
|
Nun hat man also vier Lösungen x1 ... x4. Dabei fällt auf, dass x2 und x3 ziemlich dicht beieinander liegen. Dies ist
die Umgebung der Schnittstelle von f(x) mit a(x). x1 und x4 sind die gesuchten Werte, wo die relative Abweichung zwischen f(x) und a(x) geneu gleich 1 Promille beträgt. Somit folgt, dass für alle x < x1 und alle x > x4 gilt, dass die Asymptote a(x) besser als 1 Promille mit der Funktion f(x) übereinstimmt. | |
Funktionterm aus gegebenen Eigenschaften | |
Gesucht wird der Term einer möglichst einfachen gebrochen rationalen Funktion mit folgenden Eigenschaften:
| |
| Lösung: | |
|
Gebrochen-rationale Funktionen haben die allgemeine Form: |
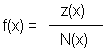
|
|
Wegen der Nullstellen müssen im Zähler der Funktion die Linearfaktoren (x-xo1) und (x-xo2) vorkommen. Also gilt die nebenstehende Gleichung: Dabei ist Z1(x) eine ganzrationale Funktion, die noch bestimmt werden muss. Egal wie Z1(x) später aussieht, f(x) hat in jedem Fall bei x = -2 und bei x = 3 je eine Nullstelle. |
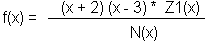
|
|
Wegen der Polstellen muss f(x) im Nenner die beiden Linearfaktoren (x-xp1) und (x-xp2) haben. Also gilt die nebenstehende Gleichung: Dabei N1(x) eine ganzrationale Funktion ist, die noch bestimmt werden muss. Egal wie N1(x) später aussieht, f(x) hat in jedem Fall bei x = -1 und bei x = 2 je eine Polstelle. |
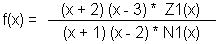
|
|
Da bei xp1 eine Polstelle ohne VZW vorliegen soll, muss der zugehörige Linearfaktor einen geraden Exponenten bekommen, und weil die Funktion möglichst einfach sein soll, wählt er die kleinstmögliche gerade Zahl, in diesem Fall also die 2. Da bei xp2 eine Polstelle mit VZW vorliegen soll, muss der zugehörige Linearfaktor einen ungeraden Exponenten bekommen, und weil die Funktion möglichst einfach sein soll, wählt er die kleinstmögliche ungerade Zahl, in diesem Fall also die 1. Und da von f(x) sonst keine Eigenchaften erwartet werden, die vom Nenner abhängen wird N1(x) = 1 gewählt. Damit ergibt sich die rechts stehende Funktion: |
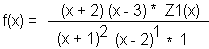
|
|
Es gilt: Grad (Z(x)) - Grad (N(x)) = Grad (ya(x)) oder Grad (Z(x)) = Grad (ya(x)) + Grad (N(x)) Da der Grad (ya(x)) = 1 und der Grad (N(x))= 3 folgt: Grad (Z(x)) = 3 + 1 = 4 und daraus wiederumf folgt, dass der Grad (Z1(x)) = 2 sein muss. Z1(x) ist also von der allgemeinen Form : Dieser Faktor im Zähler kann prinzipiell für 2 zusätzliche Nullstellen von f(x) verantwortlich sein. Daher kann man in der Aufgabenstellung die Anzahl der Nullstellen nicht einfach auf 2 begrenzen. |
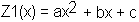
|
| Damit ergibt sich bisher für f(x): |
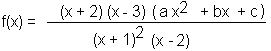
|
|
Wegen Sy = 5 folgt: f(x=0) =5 und c=5/3. |
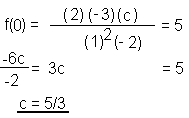
|
|
Damit hat man nun folgende Funktion: Nur die beiden Parameter a und b sind noch zu bestimmen. |

|
|
Nun hilft leider nix mehr: Zähler und Nenner müssen zunächst jeweils ausmultipliziert werden, was zwar viel Arbeit ist, keiner gerne macht, sich aber nicht länger vermeiden lässt und auch weiter nicht weh tut. Es ergibt sich: |
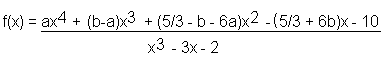
|
|
Die jetzt erforderliche Polynomdivision scheint erst einmal sehr aufwändig zu werden. Keine Angst, es wird schon werden: Wie man sieht, nach 2 Divisionsschritten ist man mit dieser Arbeit fertig. Da der Rest uninteressant ist, wird er gar nicht explizit hingeschrieben. |
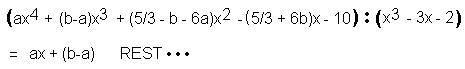
|
|
Das Ergebnis der Division ohne Beachtung des Rests entspricht also der Asymptotenfunktion: |
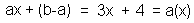
|
| Und daraus folgt endlich eindeutig, dass: |
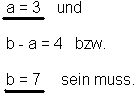
|
|
Nun sind alle Informationen beisammen, und der gesuchte Funtionsterm lautet: |
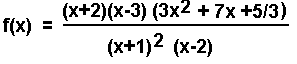
|
Der Graph von f(x) sowie seine Asymptote sind unten dargestellt. Man erkennt:
| |
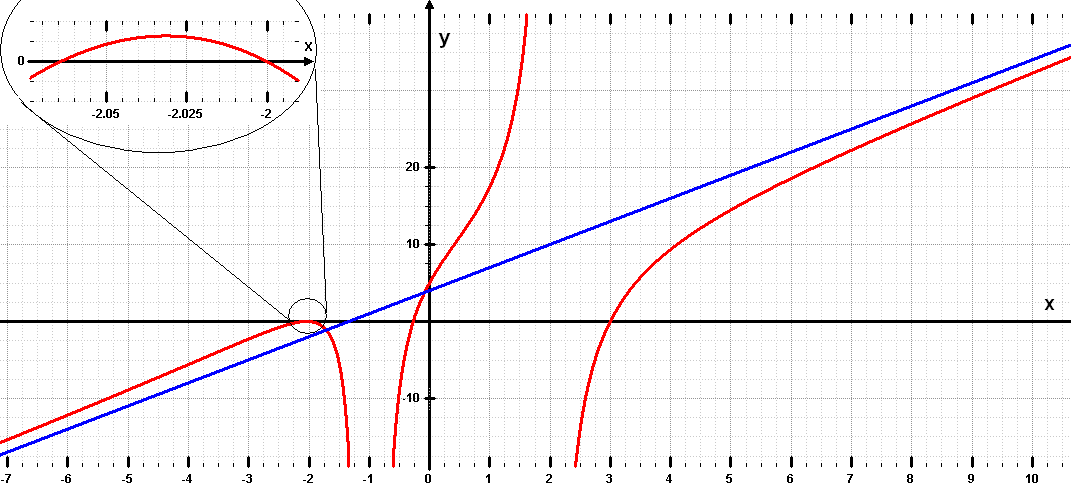
| |
|
Die beiden zusätzlichen Nullstellen waren durch die Aufgabenstellung nicht gefordert
aber auch nicht ausgeschlossen. Nun stellt sich die Frage, ob es nicht eine Funktion gibt, die die geforderten Eigenschaften hat, aber die beiden zusätzlichen Nullstellen nicht. Es lässt sich beweisen, dass dies nicht geht. (Wie denn?) Dann stellt sich allerdings die weitere Frage, wie die Aufgabenstellung sein muss, um die beiden zusätzlichen Nullstellen zu vermeiden. | |
| www.kszofingen.ch | interaktive Mathetests | www.mathe-online.at | www.ies.co.jp | engl. Mathe-Java-Applets | mathenexus.zum.de | www.arndt-bruenner.de | mathematik.zum.de | www.tutorvista.com | kostenpflichtige Nachhilfe weltweit jederzeit |
 |
vorige Seite nächste Seite |
 email an Autor |
Musterlösungen, Übersicht und Links |
 Autoelektrik Startseite |
 Berufskolleg Mitte - Essen |