n xn f(xn)
1 -1 -1,632
2 0 1,000
3 -0,5 0,107
4 -0,75 -0,653
5 -0,62 -0,231
6 -0,56 -0,056
7 -0,53 0,027
8 -0,54 0,000
9 -0,535 0,013
10 -0,537 0,008
11 -0,5385 0,004
12 -0,5378 0,006
|
Die 1. Spalte zeigt die Nummer des Iterationsschritts.
In der 2. Spalte stehen zunächst die beiden gewählten Startwerte x1 und x2 und darunter die jweiligen x-Werte der durchgeführten Iterationen.
Zu bemerken ist noch, dass ab dem 5 Schritt gar nicht immer die exakten Mittelwerte gewählt wurden, sonden x-Werte, die in der Nähe der jeweiligen
Mittelwerte liegen.
Die 3. Spalte zeigt die Funktionswerte der jeweiligen x-Werte.
Die relative Genauigkeit nach dem 12. Schritt beträgt (0,5385 -0,5378) / 0,5378 = 0,0013 = 0,13%.
Für eine geforderte Genauigkeit von 1 Promille muss noch ein weiterer Iterationsschritt folgen!
Überlegen Sie, wie sich die relative Genauigkeit bei diesem Verfahren von Schritt zu Schritt verbessert!
|


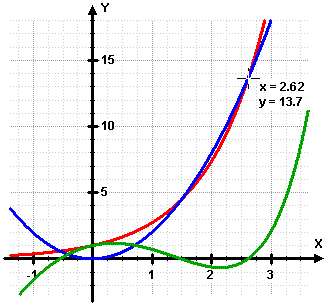
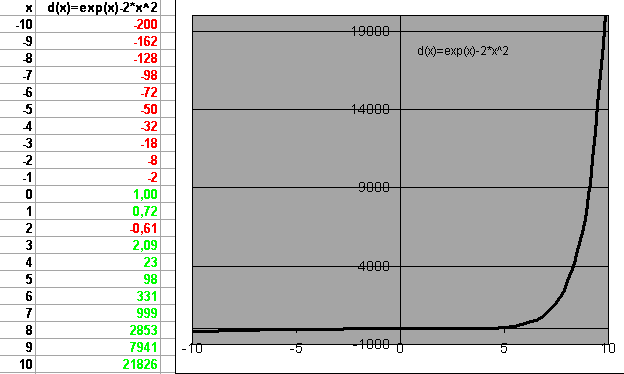 Die Skalen des Diagramms wurden angepasst. Trotzdem erkennt man die NST nicht deutlich, man ahnt nur, dass da was sein muss.
Die Skalen des Diagramms wurden angepasst. Trotzdem erkennt man die NST nicht deutlich, man ahnt nur, dass da was sein muss.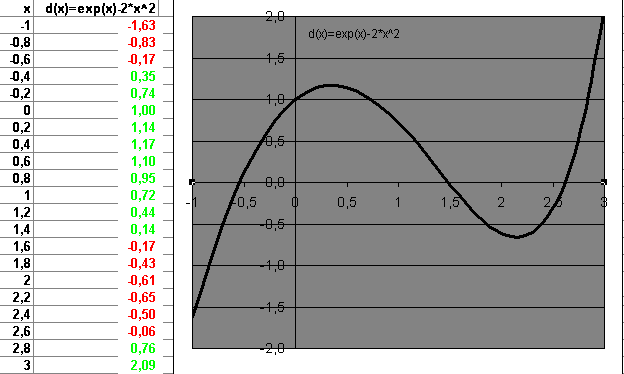 Die Mühe hat sich gelohnt. Man erkennt deutlich 3 NST. Die Form des Graphen erinnert an eine ganzrationale Funktion 3.Grades.
Tatsächlich ist es aber eine kompliziertere Funktion. Nun sollte man sich noch eine weitere Darstellung gönnen, nämlich die,
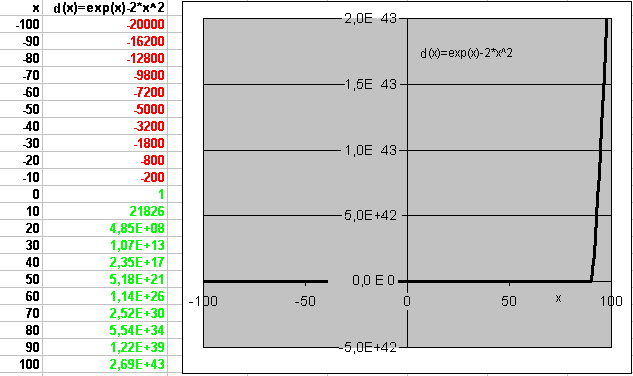
wo auch die Graphen von f(x) und g(x) dargestellt werden:
Die Mühe hat sich gelohnt. Man erkennt deutlich 3 NST. Die Form des Graphen erinnert an eine ganzrationale Funktion 3.Grades.
Tatsächlich ist es aber eine kompliziertere Funktion. Nun sollte man sich noch eine weitere Darstellung gönnen, nämlich die,
wo auch die Graphen von f(x) und g(x) dargestellt werden:
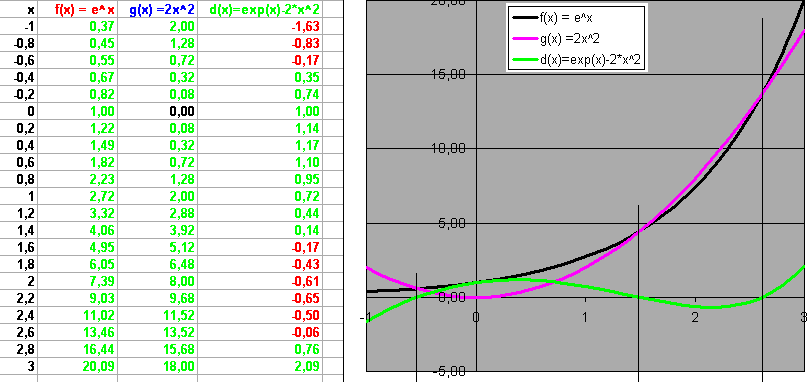 In dieser Darstellung erkennt man den Zusammenhang zwischen den NST der Differenzfunktion d(x) und den Schnittpunkten zwischen f(x) und g(x).
In dieser Darstellung erkennt man den Zusammenhang zwischen den NST der Differenzfunktion d(x) und den Schnittpunkten zwischen f(x) und g(x).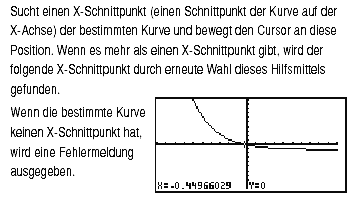 Es gibt Taschenrechner (TR), die eine sogenannte SOLVER - Funktion festprogrammiert haben.
Es gibt Taschenrechner (TR), die eine sogenannte SOLVER - Funktion festprogrammiert haben.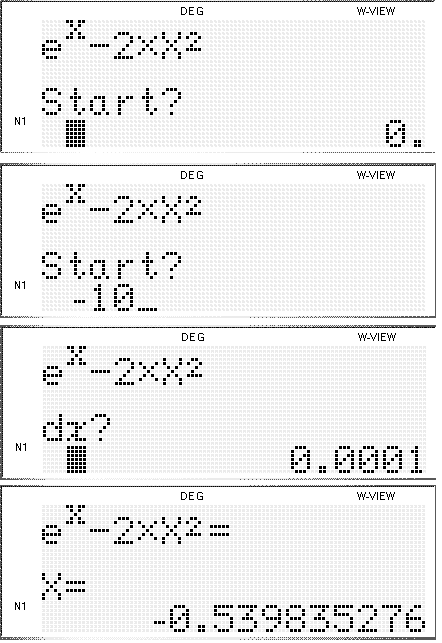 Beim TR Sharp EL-W 506 sieht das Display während der Bearbeitung der Aufgabe so aus:
Beim TR Sharp EL-W 506 sieht das Display während der Bearbeitung der Aufgabe so aus: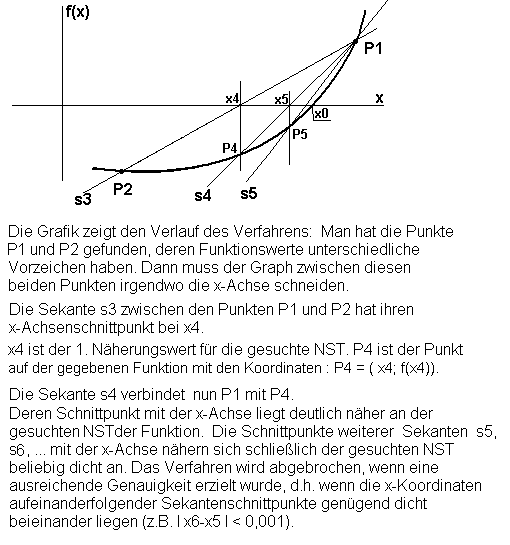 Eine ausführlichere Beschreibung findet man bei:
Nullstellenbestimmung Sekantenverfahren.
Eine ausführlichere Beschreibung findet man bei:
Nullstellenbestimmung Sekantenverfahren.
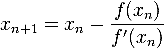 beschrieben.
beschrieben.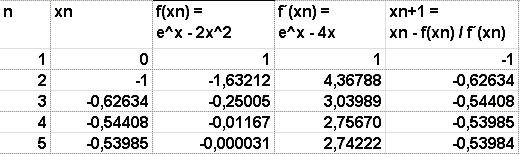 Es sind tatsächlich 15 einzelne Rechnungen zu tätigen, bevor der x6 Wert um weniger als 1 Promille von seinem Vorgänger x5 abweicht.
Es sind tatsächlich 15 einzelne Rechnungen zu tätigen, bevor der x6 Wert um weniger als 1 Promille von seinem Vorgänger x5 abweicht.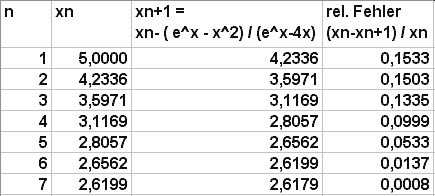 Hier ist die reduzierte Tabelle dargestellt, allerdings mit einem anderen Startwert x1 = 5.
Hier ist die reduzierte Tabelle dargestellt, allerdings mit einem anderen Startwert x1 = 5.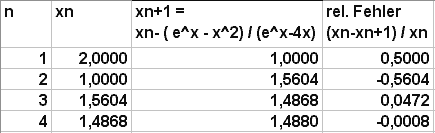 Schließlich noch die reduzierte Tabelle mit dem Startwert x1 = 2.
Schließlich noch die reduzierte Tabelle mit dem Startwert x1 = 2.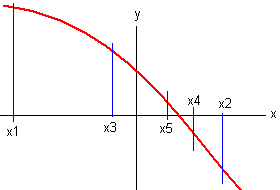 Wie beim Sekanten-Verfahren benötigt man zunächst zwei Startwerte x1 und x2, die so gewählt sein müssen, dass f(x1)< 0 und f(x2)> 0 ist.
Wie beim Sekanten-Verfahren benötigt man zunächst zwei Startwerte x1 und x2, die so gewählt sein müssen, dass f(x1)< 0 und f(x2)> 0 ist.