Einzelrechnungen |
| Beschleunigungen |
kinetische Energie für eine Beschleunigungen von 0 km/h aus 100 km/h
Ekin1 = ½ * m * v2 = ½ *1000kg * (22,2m/s)2 = 246000Nm
kinetische Energie für alle Beschleunigungen während der 100 km langen Fahrt
Ekinges = 18 * Ekin1 = 18 * 246000Nm = 4.400.000Nm
| Ekin = 4.4000.000 Nm |
| Rollreibung |
Fr = mr * m * g = 0,015 * 1000 kg * 10 m/s2 = 150N Rollreibungskraft
Er = Fr * s = 150 N * 100000m = 15000000Nm
| Er = 15.000.000 Nm |
| Luftwiderstand |
Energie zur Überwindung des Luftwiderstands
A = b * h * 0,8 = 1,7m * 1,4 m * 0,8 = 1,9m2 Widerstandsfläche
Fl = 0,62 * cw * A * v2 = (0,62 * 0,3 * 1,9 * 22,22 ) N = 174N Windwiderstandskraft
El = Fl * s = 174N * 100000m = 17400000 Nm |
El = 17.400.000 Nm |
| Steigungen |
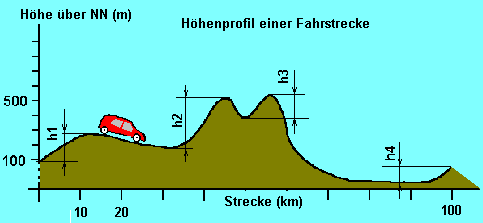
Potentielle Energie zur Überwindung aller Berge auf der Gesamtstrecke
E>pot = m* g * hges = 1000kg * 10 m/s2 * 1000m = 10000000Nm
| Epot = 10.000.000Nm |
| Nebenaggregate |
Die erforderliche Energie zum Betrieb dieser Nebenaggregate ist nur sehr aufwendig zu ermitteln. In diesem Fall soll eine pauschale Abschätzung genügen:
Klimaanlage, Servopumpe und Generator haben etwa eine gemeinsame Gesamtleistung von 5kW. Die durchschnittliche Einschaltdauer während der Fahrstrecke sei mit 0,4h angenommen.
E>neb = Pneb * te = 5kW * 0,2h = 1 kWh
1 kWh = 3.600.000 Ws = 3.600.000 Nm
| Eneb = 3.600.000 Nm |
| Motoreigenbedarf |
Der Eigenleistungsbedarf des Motors wird hier auch vereinfachend aus Erfahrungswerten zu :
Peig = 3 kW geschätzt.
Eeig = Peig * te = 3kW * 1,25h = 3,75kWh = 13500000 Nm
| Eeig = 13.500.000 Nm |
| Gesamtenergiebedarf |
Damit ergibt sich der Gesamtenergiebedarf des Fahrzeugs für diese Strecke:
Eges = Ekin + Er + El + Epot + Eneb + Eeig
Eges = 4.400.000Nm + 15.000.000Nm + 17.400.000 Nm + 10.000.000Nm + 3.600.000Nm + 13.500.000 Nm = 63.900.000Nm
| Eges = 63.900.000Nm
Eges = 63.900kJ |
| Da diese Energieangabe sehr abstrakt ist, soll nun berechnet werden, wieviel Liter Normalbenzin soviel Energie speichern. |
mbenzin = Eges / Hu = 63.900 kJ / 43000 KJ/kg = 1,5kg
Hu unterer Heizwert (Tabellenbuch), 1,5kg Benzin speichern eine Energie von 63900kJ |
und Vbenzin = mbenzin / rho = 1,5kg / 0,75 kg/l = 2 l
rho: Dichte von Benzin |
Womit als Ergebnis ein Streckenverbrauch von C= 2l / 100km berechnet wurde ??!!?? |
| Zu Recht macht das oben gedruckte Ergebnis stutzig, denn wenn es so wäre, wieso gibt es dann noch nicht längst solche Autos? Doch was soll falsch sein? Sie haben alle Angaben aus der genutzten Datenbank überprüft
und akzeptiert. Auch die Rechnungen sind korrekt. Aber die Interpretation des Ergebnisses ist falsch. Der Motor muss für die Strecke soviel mechanische Energie produzieren, wie in 2l Benzin an chemischer Energie stecken.
Das ist aber der Energieoutput des Motors. Natürlich muss wesentlich mehr als Energieinput in den Motor gefördert werden, da der Wirkungsgrad (Motor und Getriebe) leider nicht 100% beträgt. |
| Wenn man den Wirkungsgrad (eta = 23%) berücksichtigt, ergibt sich: |
Ein = E out / eta = 63900kJ / 23% = 280000 kJ
Das entspricht dem Heizwert von 6,5l Benzin |
Das Endergebnis lautet also: Bei den gegebenen Bedingungen benötigt der Pkw 6,5l Benzin auf 100km. |
| Anmerkung: Natürlich sind manche Annahmen, Rechnungen und Abschätzungen recht grob, das Ergebnis zeigt aber, dass die Gesamtüberlegungen nicht sehr weit von der Wahrheit entfernt sind. |
Datensammlung mit optimierten Werten |
| Auto |
Masse | m = 700 kg |
| Luftwiderstandsbeiwert | cw = 0,25 |
| Rollreibungszahl (trockener Asphalt) | mr = 0,013 |
| Fahrezughöhe | h = 1,3m |
| Fahrezugbreite | b = 1,5m |
| Motor | 1,8 l , 4Zyl-4-Takt-Ottomotor mittlerer Wirkungsgrad während der Fahrt (hierin sollen auch die anderen Triebwerkswirkungsgrade mitberücksichtigt sein!) | eta = 35% |
| Kraftstoff |
Dichte | rho = 0,75 kg / l |
| Heizwert | Hu = 43000 kJ /kg |
| Strecke |
Länge der Fahrstrecke | s = 100 km |
| Gesamthöhe aller zu überwindenden Steigungen | hges = 1000 m |
| Fahrweise |
Durchschnittsgeschwindigkeit | vges = 80 km /hl |
| Beschleunigungen | 4 mal 0 km/h -> 100 km/h und 40 mal 80 km/h -> 120 km/h |
Zusätzlich: Nebenaggregate werden seltener genutzt: (8% der Fahrzeit)
Der Motor arbeitet im Intervallbetrieb: Wenn er gebraucht wird arbeitet er unter Volllast, sonst ist er abgeschaltet.
Man kommt auf etwa 50% Einschaltdauer des Motors während der Fahrt.
-
Vorteile:
- höherer Wirkungsgrad.
- kein Eigenenergieverbrauch ohne Nutzenergieabgabe.
-
Nachteile: ...
|



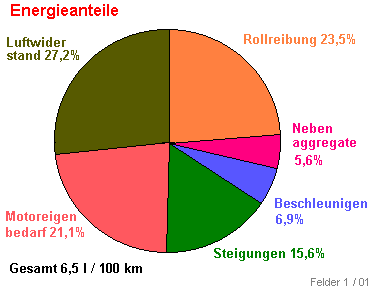 Dieses Kreisdiagramm zeigt deutlich die Anteile der einzelenen Elemente am
Gesamtkraftstoffverbrauch.
Dieses Kreisdiagramm zeigt deutlich die Anteile der einzelenen Elemente am
Gesamtkraftstoffverbrauch.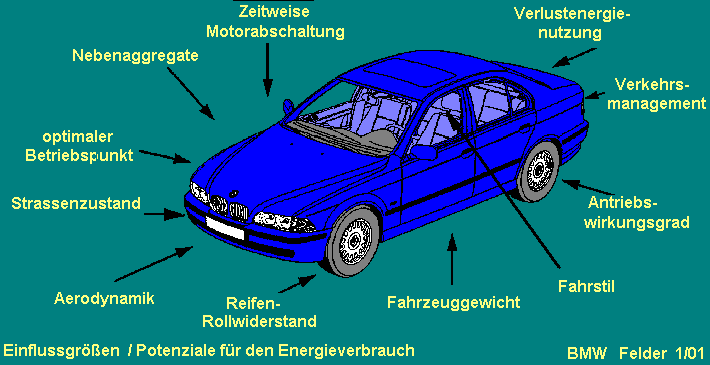 In der Grafik links werden alle Einflussfaktoren für den Kraftstoffverbrauch eines Fahrzeugs zusammengefasst.
In der Grafik links werden alle Einflussfaktoren für den Kraftstoffverbrauch eines Fahrzeugs zusammengefasst.