|
Arbeitspunkt
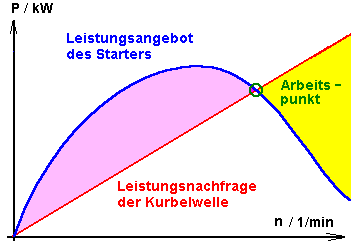
Bei Leistungsgleichgewicht oder Drehmomentgleichgewicht steht zur Beschleunigung keine Reserve mehr zur Verfügung und die
Drehzahl kann ncht weiter steigen.
Umgekehrt ist in diesem die Kurbelwelle aber zum Abbremsen des Starters zu schwach, so dass die Drehzahl auch nicht fällt, sie bleibt also konstant.
Diese im Gleichgewicht oder im Arbeitspunkt erreichte Drehzahl muss über der Startmindestdrehzahl des Verbrennungsmotors liegen,
andernfalls ist die Starter-Akku-Kombination zu schwach ausgewählt. Liegt jedoch diese Drehzahl weit über der Startmidestdrehzahl,
so ließe sich erwägen, einen kleineren Starter oder eine schwächere Batterie einzusetzen (Kosten- u. Gewichtsvorteile)
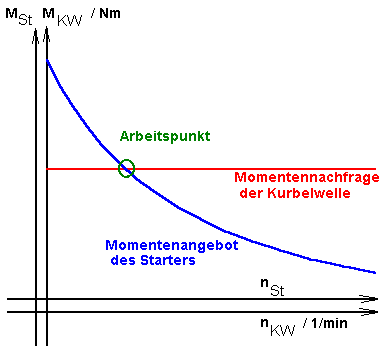
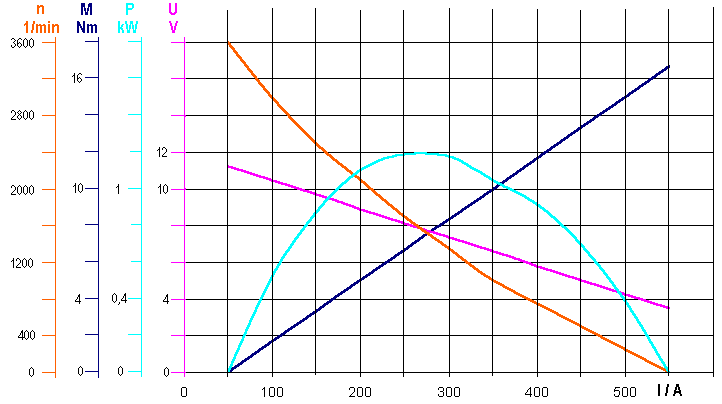
Im Starterkennlinienfeld bezeichnet man mit dem Arbeitspunkt gerade die Bedingungen
(I, M, n, P, U, h), die im stationären Fall gelten.
Die zum Arbeitspunkt gehörenden Werte liegen im Kennlinienfeld des Starters alle auf einer senkrechten Linie bei I(AP)
Zur Wahl des Arbeitpunktes gelten folgende Regeln:-
AP stets in der Nähe des größten Wirkungsgrades legen
-
AP so legen, dass I klein bleibt (Belastung von Akku Leitungen und Starter)
-
AP stets zwischen dem berechneten Pmin und Pmax plazieren
-
Je näher AP bei Pmax liegt, umso kleiner wird der Schwungscheibendurchmesser
-
Je näher AP bei Pmin liegt, umso schneller wird AP erreicht
-
AP liegt stets bei Drehzahlen, die höher sind als die Drehzahl bei Pmax .
Nicht alle Bedingungen lassen sich gleichzeitig erfüllen!
|
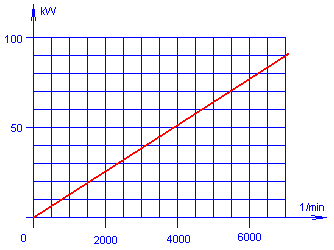 Diese Leistung lässt sich mit der Formel berechnen:
Diese Leistung lässt sich mit der Formel berechnen: