Musterlösungen, Übersicht und Links

Musterlösungen

Berufskolleg Mitte - Essen

vorige Seite

4.0102 Anwendungen der Integralrechnung

Weltbevölkerung

nächste Seite

1. Aufgabe

Wie viel % aller Menschen, die jemals auf dieser Erde gelebt haben, leben eigentlich immer noch?

2. Lösung

Vorbemerkung: Auf dieser Seite wird nur eine grobe Abschätzung zur Aufgabe erarbeitet.
Es müssen dazu viele Annahmen gemacht werden, da reale Daten nicht vefügbar sind.
Trotz allem, die prinzipielle Lösung ist verblüffend und dürfte nicht all zu weit vom tatsächlichen Wert abweichen.

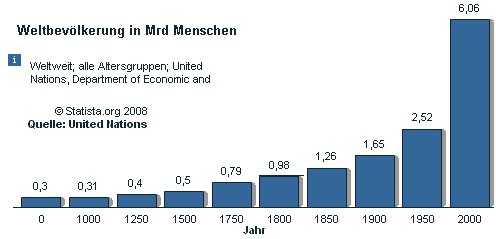Auf der Erde lebten im Jahre 2000 etwa 6,06 Mrd Menschen. Um 1000 waren es nur 0,31 Mrd Menschen.
Diese Zahlen findet man z.B. bei http://de.statista.org.

Wir nehmen einmal an, dass sich die Weltbevölkerung in den letzten 2000 Jahren gemäß einem einfachen exponentiellem Wachstum entwickelt hat:

N(t) = No * exp (w*t)

(Tatsächlich hat sich auch der Wachstumsexponent w mit der Zeit vergrößert)

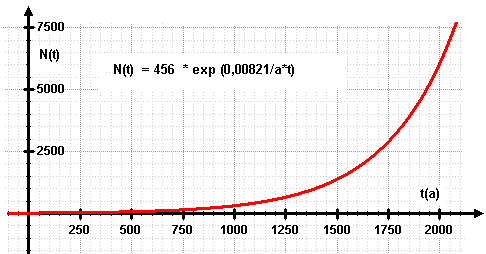Mit diesen Angaben lässt sich nun No und w bestimmen: (Ihre Aufgabe)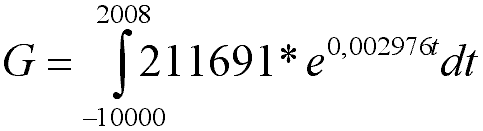

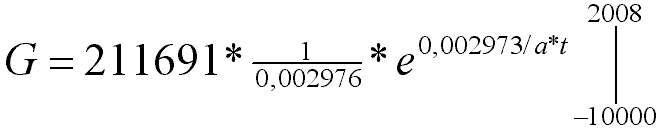
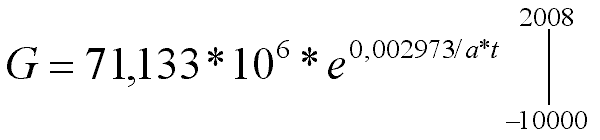
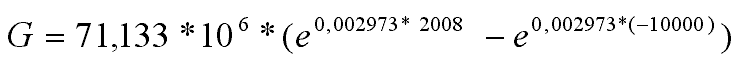
No = 15,86 Mio (Weltbewohner zur Zeit Christi !!??? s. Annahme)
w = 0,002973/a (Wachstumsrate pro Jahr)

Damit gelte also

N(t) = 456 * exp (0,00821/a*t)

Die Koeffizienten No und w wurden so berechnet, dass die Funktionswerte in den beiden Jahren 1000 und 2000 nach Christi mit den Statistikwerten übereinstimmen.
Für alle anderen Jahre weichen die Ergebnisse der Modellrechnung von den Statistikwerten ab.

Derzeit rechnet man mit 2,6 Geburten/s weltweit, was 81,94 Mio Geburten / Jahr entspricht! (s. www.weltbevoelkerung.de)

Unter der nächsten verwegenen Annahme, dass alle Menschen immer im selben Alter gestorben sind, kann man dann auch für die Anzahl der Geburten/s eine zeitl. Funktion aufstellen, wobei der Wachstumsfaktor w im Exponenten wieder w= 0,002973 beträgt. n(t) = no * exp ( 0,002973/a*t)

Mit der Angabe lässt sich no berechnen:
no = 81400000/a / exp (0,002973/a*2000a) = 211691/a

Im selben Jahr, als Jesus geboren wurde, wurden weitere 211690 Babies weltweit geboren (so diese Rechnung!).

Also gilt nun die Gleichung:

n(t) = 211691/a * exp(0,002973/a*t)

Nun hat man eine Funktion, mit der man die Anzahl der Menschen berechnen kann, die in jedem Jahr geboren wurden. Addiert man alle diese Zahlen seit seit den letzten ca 10000 Jahren, so weiß man, wie viele Menschen insgesamt auf der Erde bisher jemals gelebt haben.

Anstelle der Summenbildung wird hier durch das Integral die Summe aller Geburten von 10000 vor Christi bis 2008 nach Christi Geburt berechnet:

G = 27,84 Mrd

So viele Menschen wurden bis zum Jahr 2008 (nach dieser Rechnung) auf der Welt insgesamt geboren.

Von diesen 27,84Mrd Menschen leben heute noch 6,06 Mrd. Das ist ein Anteil von etwa 22%.

Von allen Menschen, die jemals auf der Erde gelebt haben, leben heute etwa 22% !

Zusatzaufgabe:
Nehmen Sie an, alle Menschen werden gleich alt. Wie groß ist dann die Lebenserwartung für jeden?
Lösung ca. 82,5 Jahre !!

vorige Seite

nächste Seite

email an Autor

Musterlösungen, Übersicht und Links

Autoelektrik Startseite

Berufskolleg Mitte - Essen