Seitenende Autoelektrik ( Startseite)

Musterlösungen, Übersicht und Links

Musterlösungen

Berufskolleg Mitte - Essen
vorige Seite

3.16 Bestimmung ganzrationaler Funktionen aus vorgegebenen Eigenschaften

 nächste Seite

















1. Aufgabe





2. Aufgabe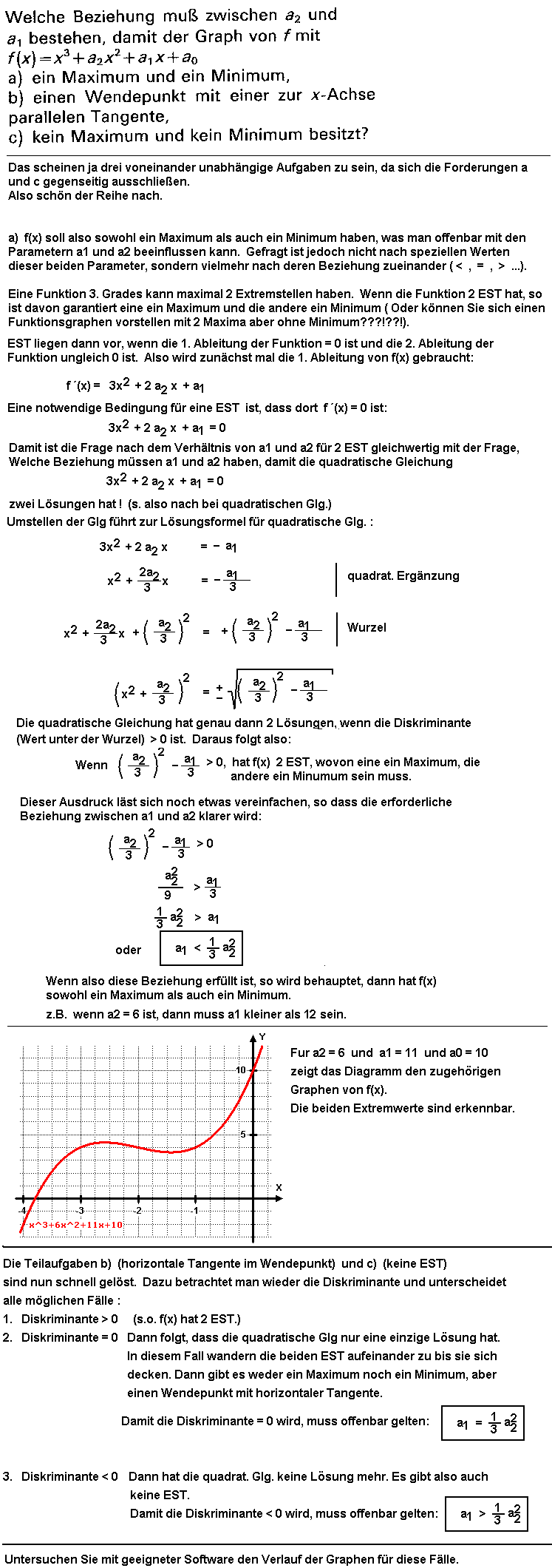










3.Aufgabe


Der Graph einer punktsymmetrischen Funktion 5.Grades hat
im Nullpunkt einen Sattelpunkt und
bei x=2 eine Wendestelle mit der Steigung mt = 1.
Bestimmen Sie den Funktionsterm!


Die Schwierigkeiten bei solchen Aufgaben bestehen darin,
  1. aus dem Text alle Informationen herauszufinden,
  2. zu diesen Informationen passende Gleichungen zu formulieren, und
  3. das so entstandene Gleichungssystem zu lösen.


Sie müssen sich darauf verlassen können, dass im Aufgabentext alle erforderlichen
Informationen stecken und die Aufgabe (meistens) eindeutig lösbar ist.

Lösung:

Information aus Aufgabenstellung zugehörige mathematische Gleichung Kommentar
... Funktion 5. Grades... f(x) = a*x5 + b*x4 + c*x3 + d*x2 + e*x1 + f gemeint ist offenbar eine ganzrationale Funktion.
"5.Grades" bedeutet, dass der höchste Exponent 5 ist,
dass also a auf jedenfall ungleich 0 sein muss und
und dass zunächst mal alle anderen Koeffizienten (b,c,d,e,f) auch ungleich 0 sein können.
... punktsymmetrisch... f(x) = a*x5 + c*x3 + e*x1 Eine Funktion genau dann punktsymmetrisch, wenn nur ungerade Exponenten von x im Funktionsterm vorkommen.
Die Koeffizienten b, d und f müssen also = 0 sein.
Das erspart aber auch viel Arbeit, denn nun sind nur noch die 3 Unbekannten a, c und e zu ermitteln.
... hat im Nullpunkt einen Sattelpunkt... f(0) = 0
f(0) = a*05 + c*03 + e*01 = 0
0 = 0*a + 0*c + 0*e 		Der Funktionsgraph verläuft durch den Koordinatenursprung (0;0), weil er ja dort einen Sattelpunkt hat.
Daraus folgen die links stehenden Gleichungen.
Leider kann man aus diesen Gleichungen keinerlei Nutzen ziehen.(Schade!)
Denn 0 = 0 ist trivial.
... hat im Nullpunkt einen Sattelpunkt... f´(0) = 0 = 5a*04 + 3c*02 + e

=>

e = 0

Für einen Sattelpunkt gilt: f´(xs) = 0
Ein Sattelpunkt hat also eine horizontale Tangente.
Damit ist also der Koffizient e nun bekannt.
Da e = 0, vereinfacht sich die Funktionsgleichung zu:
f(x) = a*x5 + c*x3
Die beiden Unbekannten a und c sind noch zu bestimmen.
... hat im Nullpunkt einen Sattelpunkt... f´´(0) = 0 = 20a*03 + 6c*01 Für einen Sattelpunkt gilt außerdem: f´´(xs) = 0
Im Sattelpunkt hat der Graph auch keine Krümmung, bzw. eine Wendestelle. Leider kann man aus diesen Gleichungen keinerlei Nutzen ziehen.(Schade!)
Denn 0 = 0 ist trivial.
...hat bei x=2 eine Wendestelle... f´´(2) = 0 = 20a*23 + 6c*21
f´´(2) = 0 = 160a + 12c
160a + 12c = 0

An einer Wendestelle ist die 2. Ableitung der Funktion =0.
Somit hat man eine schöne Gleichung mit den beiden Unbekannten a und c.
Um 2 Unbekannte zu berechnen, benötigt man aber 2 geeignete Gleichungen.
Also muss man weitersuchen, um die 2. erforderliche Gleichung zu finden.
...mit der Steigung mt = 1... f´(2) = 1 = 5a*24 + 3c*22
f´(2) = 1 = 80a + 12c
80a + 12c = 1 		Die Steigung bei x = 2 soll also 1 sein.
D.h., dass die 1. Ableitung der Funktion für x = 2 den Wert 1 haben soll.
Daraus wird die 2. erforderliche Gleichung für die beiden Unbekannten a und c gestrickt.

80a + 12c = 1
160a + 12c = 0 		Nun hat man ein Gleichungssystem von 2 Gleichungen mit 2 Unbekannten.
Dieses ist mit einem modernen TR recht einfach lösbar.
Natürlich kann man auch ohne TR die Werte von a und c berechnen.

a = -0,0125
b = 0,166666

 Es ergeben sich für a und c die angegebenen Werte.

f(x) = -1/80 * x5 + 1/6 * x3 Damit ist der gesuchte Funktionsterm bestimmt.
Eine Probe ist unbedingt erforderlich, wer ist sich schon so sicher, dass er darauf verzichten könnte.
Üblicherweise ist der Funktionsterm dazu auf die verlangten Eigenschaften zu prüfen (durch NACHRECHNEN)
Ein Funktionsplotter erleichtert einem diese Sache jedoch sehr:
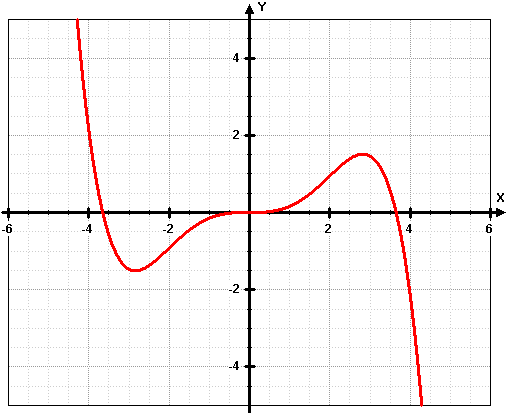Eine Grafik kann kein Beweis sein, schon allein wegen er darin enthaltenen Ungenauigkeiten.
Trotzdem:
Auf den 1. Blick scheint der Funktionsgraph punktsymmetrisch zu sein.
Er durchläuft den Punkt (0;0)
Er hat dort einen Sattelpunkt (Wendestelle mit horizontaler Tangente).
Er hat bei x = 2 eine Steigung von etwa 45° (Steigung = 1).
Am Funktionsterm erkennt direkt den Grad : 5.


Mit diesem starken Indiz für die Richtigkeit der Lösung geben wir uns heute mal zufrieden.








4.Aufgabe


Der 2,1L-4-Zyl-Diesel-Motor von Mercedes hat
sein größtes Drehmoment von 500Nm bei einer Drehzahl von 1620/min und
seine maximale Leistung von 150kW bei einer Drehzahl von 4200/min.
Bestimmen Sie die Funktionsterme M(n) und P(n)!


Nutzen Sie zur Lösung dieser Aufgabe ganzrationale Funktionen mit möglichst kleinem Grad.

Lösung:

Information aus Aufgabenstellung zugehörige mathematische Gleichung Kommentar
Mmax= 500Nm (1600/min) M(27) = 500 Die Drehzahlen werden bei der Lösung der Aufgabe in der Einheit 1/s angegeben, in Übereinstimmung mit dem SI.
In den Berechnungen werden die Einheiten nicht mitgeschrieben. Es sind aber stets die zugehörigen SI Einheiten gemeint.
Der Funktionsgraph von M(n) läuft also durch den Punkt (27 ; 500).
Mmax= 500Nm (1600/min) M´(27) = 0 Am Drehmomentmaximum hat der Graph von M(n) eine horizontale Tangente.
Pmax= 150kW (4200/min) P(70)=150000 Wieder wurde die Drehzahlangabe in 1/s gemacht.
Die SI-Einheit der Leistung ist das Watt.
Der Funktionsgraph von P(n) läuft also durch den Punkt (70 ; 150000).
Pmax= 150kW (4200/min) P´(70) = 0 Am Leistungsmaximum hat der Graph von P(n) eine horizontale Tangente.
aus der Allgemeinbildung oder der Formelsammlung P = M * n * 2 * pi Dieser Zusammenhang zwischen Drehmoment, Leistung und Drehzahl gilt für alle drehenden Maschinen, also auch für Kurbelwellen im Dieselmotor.
Diese Formel sollte jedem kfz-Mechatroniker bekannt sein.
in der Formelsammlung findet man häufig die zugeschnittene Größengleichung
P = M * n /9550,
die gilt, wenn man P in kW und n in 1/min einsetzt (wollen wir hier aber nicht).
Soweit die Ausgangslage.
Die ersten 4 Gleichungen haben etwas mit den Funktionsgraphen zu tun, die letzte jedoch nicht.
So stehen 4 Gleichungen zur Verfügung, mit denen sich 4 Unbekannte berechnen lassen.
4 Unbekannte bzw. 4 Parameter, dass stinkt nach einer ganzrationalen Funktion 3. Grades.
Bleibt die Frage, ob M(n) 3. Grades sein soll oder P(n) oder beide??
Probieren!!
Zunächst soll also M(n) mal eine Funktion 3. Grades sein. M(n) = a * n3 + b * n2 + c * n + d Die 4 Parameter sind also a, b, c und d.
Diese sollen ermittelt werden können!?!?!
Wenn man die Funktion M(n) kennt, kann man aus der Beziehung zwischen M, n und P auch die Funktion P(n) ermitteln (oder auch umgekehrt).
M(27) = 500 M(27) = 500 = a * 273 + b * 272 + c * 27 + d
19683a + 729b + 27c + d = 500 		Damit hat man eine Gleichung von vieren fertig.
M´(27) = 0 M´(n) = 3 a * n2 + 2b * n + c
M´(27) = 3 a * 272 + 2b * 27 + c = 0
M´(27) = 2187 a + 54b + c = 0
2187a + 54b + c = 0 		Damit hat man eine weitere Gleichung von vieren fertig.
Mit
P = M * n * 2 * pi
folgt auch, dass
P(n) = M(n) * n * 2 * pi 		P(n) = ( an3 + bn2 + cn + d ) * 2n*pi

oder

P(n) = ( an4 + bn3 + cn2 + dn ) * 2pi

 Weil man mit der Formel P=M*n*2*pi für bestimmte Werte von n und M die jeweilige Leistung ausrechnen kann, kann man genau so gut gleich die komplette Funktion P(n) bestimmen, wenn man die Funktion M(n) kennt.
P(70)=150000 P(70) = ( 704a + 703b + 702c + 70d ) * 2*pi = 150000

oder

704a + 703b + 702c + 70d = 23873
 Damit hat man die 3. erforderliche Gleichung von vieren fertig.
P´(70) = 0 P´(n) = (4an3 + 3bn2 + cn) * 2pi
P´(70) = (4*703a + 3*702b + 2*70c + d) * 2pi = 0

oder

4*703a + 3*702b + 2*70c + d = 0 		Das ist die 4. erfoderliche Gleichung.
Die 4 Gleichungen, mit denen die 4 Unbekannten a, b, c und d berechnet werden können heißen also: (I): 19683a + 729b + 27c + d = 500
(II): 2187a + 54b + c = 0
(III): 704a + 703b + 702c + 70d = 23873
(IV): 4*703a + 3*702b + 2*70c + d = 0
 		Dieses lineare Gleichungssystem aus 4 Gleichungen mit 4 Unbekannten muss zunächst reduziert werden auf ein System aus 3 Gleichungen mit 3 Unbekannten, bevor dieses dann mit einem "intelligenten" TR schnell gelöst werden kann.
Ohne TR ist es natürlich auch lösbar, dauert aber länger.
Man kann Gl. (IV) von Gl.(I) subtahieren und d fällt weg.
Wenn man Gl (IV) mit 70 multipliziert und dann von Gl. (III) subtrahiert, erhält man ebenfalls eine Gl. ohne d.
Schließlich ist in Gl (II) auch kein d enthalten.
so hat man folgende 3 Gleichungen: 		-1352317a - 13971b - 113c = 500

72030000a - 686000b - 4900c = 23873

2187a + 54b = 0 		Damit hat man das erwünschte lineare Gleichungssystem aus 3 Gleichungen mit den 3 Unbekannten a, b und c.
Diese 3 Gleichungen ergeben: a = 0,001364
b = -0,2551
c = 10,79 		Die Gl. (I) kann man nach d umstellen und die nun bekannten Werte für a, b und c einsetzen und erhält :

d = 367,8
Damit hat man alle 4 gesuchten Parameter zusammen und kann die Funktionsgleichungen angeben.

M(n) = 0,001364n3 - 0,2551n2 + 10,79n + 367,8

P(n) = (0,001364n4 - 0,2551n3 + 10,79n2 + 367,8n ) * 2pi

Die gesuchten Funktionsgleichungen für M(n) und P(n) sind damit gefunden!

Diese Lösung bedarf noch einer ordentlichen Probe.

geprüft werden können alle 4 Bedingungen, die in der Aufgabenstellung gegeben waren:
  1. Der Graph von M(n) verläuft durch den Punkt (27 ; 500).
  2. Der Graph von P(n) verläuft durch den Punkt (70 ; 150000).
  3. Der Graph von M(n) hat bei n = 27 ein Maximum.
  4. Der Graph von P(n) hat bei n = 70 ein Maximum.

Probe1


 M(27) = 0,001364 * 273 - 0,2551 * 272 + 10,79 * 27 + 367,8

M(27) = 500,0097 (500)

Probe2


 M´(27) = 3* 0,001364 * 272 - 2 *0,2551 * 27< + 10,79

M´(27) = -0,00233 (0)

Probe3


 P(70) = (0,001364 * 704 - 0,2551 * 703 + 10,79 * 702 + 367,8 * 70 ) *2pi

P(70) = 149963 (150000)

Probe4


 P´(70) = (4 * 0,001364 * 703 - 3 * 0,2551 * 702 + 2 * 10,79 * 70 + 367,8) * 2pi

P´(70) =-1,018 (0) !!
Proben 1, 2 und 3 waren erfolgreich (kleine Rundungsfehler sind nicht zu vermeiden).
Bei Probe 4 ist nicht klar, ob die Abweichung vom erwarteten Wert toleriert werden kann. (Das Maximum der verwendeten Funktion liegt bei 69,967!)
Daher (und sowieso wegen der Anschaulichkeit) sollen nun auch noch die Graphen gezeigt werden.
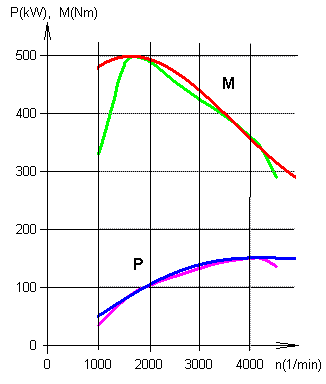Dargestellt sind in den Farben grün und pink der Drehmoment- / Leistungsverlauf als Funktion der Drehzahl, so wie es von einer Graphik in der amz 8/09 übertragen wurde.

In den Farben rot und blau sind die Graphen M(n) bzw. P(n) dargestellt, wie sie sich aus den berechneten Funktionstermen ergeben.
Diese beiden Graphen sind an die Drehzahlskala in der Einheit 1/min angepasst worden.

Die tatsächliche Abhängigkeit des Drehmoments von der Drehzahl entspricht offenbar nicht der ganzrationalen Funktion 3. Grades.
Aber sowohl die beiden Graphen fürs Drehmoment als auch die für die Leistung haben im Drehmomentmaximum und im Leistungsmaximum gleiche Werte, wie man es auch erwartet hat, da ja die theoretischen Funktionen gerade auf diesen Werten basieren.








5. Aufgabe

Der Graph einer ganzrationalen Funktion 5. Grades geht durch den Ursprung,
hat in W1 (-1; -2/3) einen Wendepunkt mit der Steigung der zugehörigen
Wendetangente m1 = 1,25 und einen weiteren Wendepunkt W2(-2; -4/3).
Wie lautet die Funktionsgleichung dieser Funktion?

Lösung:
Die allgemeine Form einer ganzrationalen Funktion 5. Grades lautet:
f(x) = ax5 + bx4 + cx3 + dx2 + ex + f
mit den 6 unbekannten Koeffizienten a, b, c, d, e und f.
Diese sollen hier berechnet werden.

Dazu benötigt man 6 geeignete Gleichungen.
Diese muss man aus den gegebenen Eigenschaften der Funktion herleiten können, was an sich bereits eine gewisse Kunst ist:
1. ... GEHT DURCH DEN URSPRUNG ... bedeutet, dass f(0) = 0 ist.
Setzt man das also in die allgemeine Funktionsgleichung ein, erhält man:
f(0) = a05 + b04 + c03 + d02 + e0 + f = 0
Und aus dieser Gleichung folgt:
f = 0, womit bereits eine der 6 unbekannten Größen gefunden wurde.
Damit reduziert sich die Funktionsgleichung auf:
f(x) = ax5 + bx4 + cx3 + dx2 + ex

2. ... HAT IN W1 (-1; -2/3) EINEN WENDEPUNKT ... bedeutet zunächst, dass der Graph von f(x) durch diesen Punkt läuft.
Damit gilt:
f(-1) = a(-1)5 + b(-1)4 + c(-1)3 + d(-1)2 + e(-1) = -2/3
oder ausgerechnet:
-a + b -c + d - e = -2/3
Dies ist eine von 5 Gleichungen, mit denen die Unbekannten a ... e berechnet werden können sollen.
4 weitere Gleichungen sind also noch zu finden!

3. ... WEITEREN WENDEPUNKT W2 (-2; -4/3) ... hat zunächst die entsprechende Bedeutung wie oben:
f(-2) = a(-2)5 + b(-2)4 + c(-2)3 + d(-2)2 + e(-2) = -4/3
oder ausgerechnet:
-32a + 16b -8c + 4d - 2e = -4/3
oder durch 2 gekürzt:
-16a + 8b -4c + 2d - e = -2/3

4. ...STEIGUNG DER WENDETANGENTE m1 = 1,25 ... heißt im Klartext, dass die 1. Ableitung der Funktion an der Stelle x= -1 gleich 1,25 ist, also als Formel:
f´(-1) = 1,25
f´(x) = 5ax4 + 4bx3 + 3cx2 + 2dx + e
Und wenn man dafür die gegebenen Werte nutzt, erhält man
5a(-1)4 + 4b(-1)3 + 3c(-1)2 + 2d(-1) + e = 5/4 (da 1,25 = 5/4)
oder:
5a - 4b + 3c - 2d + e = 5/4

womit bisher also 3 von 5 erforderlichen Gleichungen gefunden sind.

5.... HAT IN W1 (-1; -2/3) EINEN WENDEPUNKT ... bedeutet zusätzlich, dass dort die 2. Ableitung der Funktion 0 sein muss.
f´´(-1) = 0
f´´(x) = 20ax3 + 12bx2 + 6cx + 2d
Werte einsetzen: f´´(-1) = 20a(-1)3 + 12b(-1)2 + 6c(-1) + 2d = 0
oder
-20a + 12b - 6c + 2d = 0
durch 2 gekürzt:
-10a + 6b - 3c + d = 0

6. ... WEITEREN WENDEPUNKT W2 (-2; -4/3) ... , na Sie wissen schon.
f´´(-2) = 0
f´´(-2) = 20a(-2)3 + 12b(-2)2 + 6c(-2) + 2d = 0
-160a + 48b - 12c + 2d = 0
-80a + 24b - 6c + d = 0


Die 5 gefundenen Bestimmungsgleichungen werden hier noch einmal übersichtlich und durchneummeriert aufgeschrieben:

  I  -  a +   b - c  +  d - e = -2/3
 II  -16a +  8b - 4c + 2d - e = -2/3
III    5a -  4b + 3c - 2d + e =  5/4
 IV  -10a +  6b - 3c +  d     =  0
  V  -80a + 24b - 6c +  d     =  0
Man hat hier ein lineares Gleichungssystem mit 5 Gleichungen und 5 Unbekannten.
Dies ist Schritt für Schritt zu reduzieren zunächst auf ein S Wenn das geschafft ist, hilft ein geeigneter Taschenrechner weiter.

Wenn man z.B. Gleichung I und Gleichung III addiert, fällt e weg.
Ebenso bei Gleichung II und III.
Dann hat man das zunächst reduzierte 4er-System: 

 I+III  (VI)   4a -  3b + 2c - d =  7/12
II+III (VII) -11a +  4b -  c     =  7/12
         IV  -10a +  6b - 3c + d =  0
          V  -80a + 24b - 6c + d =  0
mit den 4 Unbekannten a, b, c und d

Addiert man hier einerseits Gl. IV mit Gl. VI und andererseits Gl. IV mit Gl. V,
so hat man d eliminiert und ein Gleichungssystem aus 3 Gleichungen mit 3 Unbekannten:

-11a +  4b -  c =  7/12
- 6a +  3b -  c =  7/12
-76a + 21b - 4c =  7/12
Wer´s bis hierhin geschafft hat, wird nun erleichtert die Hilfe des TR in Anspruch nehmen dürfen.
(z.B. Sharp EL-W506)
Mit MODE 6, 1 springt der TR in das Lösungsprogramm für 3 Gl. mit 3 Unbekannten.
Einzugeben ist nun: 

a1 = -11   b1 =  4   c1 = - 1   d1 =  7/12
a2 = - 6   b2 =  3   c2 = - 1   d2 =  7/12
a3 = -76   b3 = 21   c3 = - 4   d3 =  7/12
Dann liefert der TR folgende Ergebnisse:
x= 1/4, y= 5/4, z= 4/3,
wobei man nun wissen muss, dass der TR mit x,y und z bezeichnet, was in unserer Aufgabe mit a, b und c bezeichnet wurde.
Damit sind also endlich die 3 Unbekannten a, b und c berechnet:
 a= 1/4;    b = 5/4;   c = 4/3
Da f schon lange bekannt ist (f=0), fehlen noch die 2 Koeffizienten d und e.
Suche also weiter oben bereits notierte Gleichungen, die du dazu nutzen kannst.
z.B. mit  Gl.VI   4a -  3b + 2c - d       =  7/12
und  mit  Gl. I  -  a +   b - c  +  d - e = -2/3
lässt sich erst d berechnen und anschließend e.
Die Rechnung ergibt :
d = e = 0, beide Werte sind 0.
Damit lautet die Funktionsgleichung mit den gegebenen Eigenschaften:

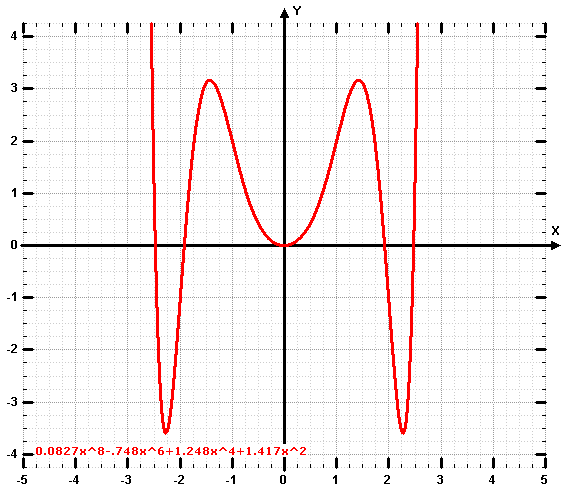
f(x) = 1/4x5 + 5/4x4 + 5/3x3

Der Graph von f(x) wird hier rot dargestellt:
Die blaue Linie ist Wendetangente von W1. 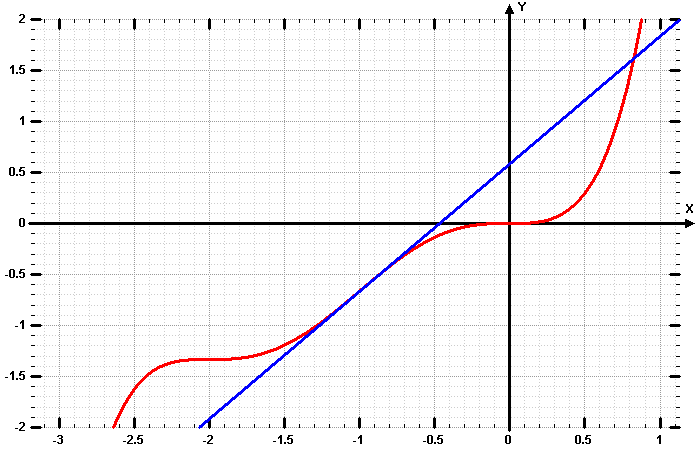Graph von f(x)


5. Aufgabe

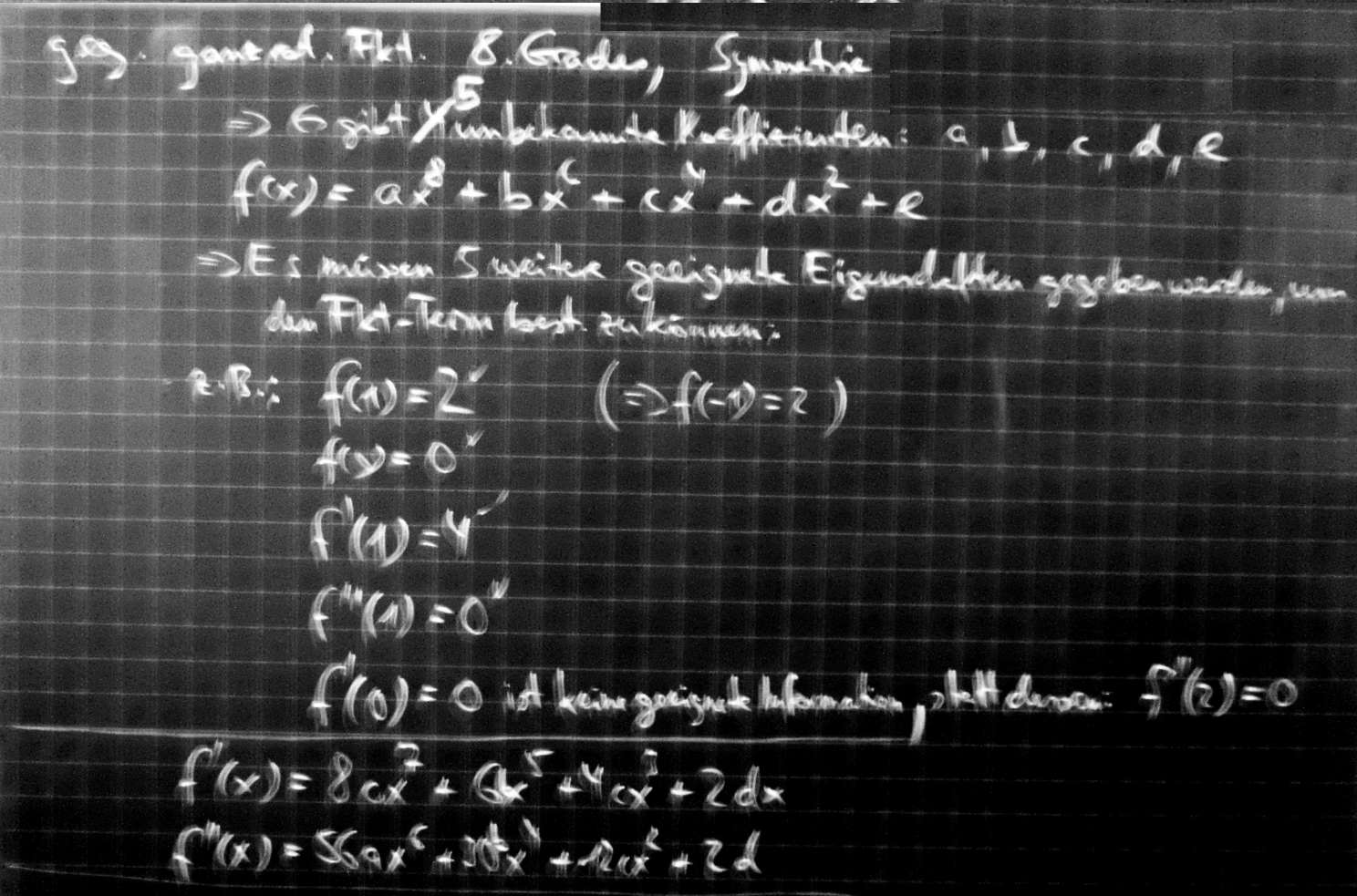
Selbst konstruierte Aufgabe 8.Grades achssymmetrisch, Tafelbild
Selbst konstruierte Aufgabe 8.Grades achssymmetrisch, Tafelbild
Selbst konstruierte Aufgabe 8.Grades achssymmetrisch Funktionsgraph





Hier sind einige Links zu finden, die zu interessanten / hilfreichen Matheseiten im WWW führen.

www.kszofingen.ch interaktive Mathetests
www.mathe-online.at
www.ies.co.jp engl. Mathe-Java-Applets
mathenexus.zum.de
www.arndt-bruenner.de
mathematik.zum.de
www.tutorvista.com kostenpflichtige Nachhilfe weltweit jederzeit










Seitenanfang vorige Seite

nächste Seite		 eMail an Autor
email an Autor

Musterlösungen, Übersicht und Links

 Startseite
Autoelektrik Startseite

Berufskolleg Mitte - Essen