Musterlösungen, Übersicht und Links
Musterlösungen
Berufskolleg Mitte - Essen
|
|
Autoelektrik ( Startseite) Musterlösungen, Übersicht und LinksMusterlösungen |
Berufskolleg Mitte - Essen |
|
| vorige Seite | 1.14 Lineare Funktionen |
nächste Seite |
1. Aufgabe | |||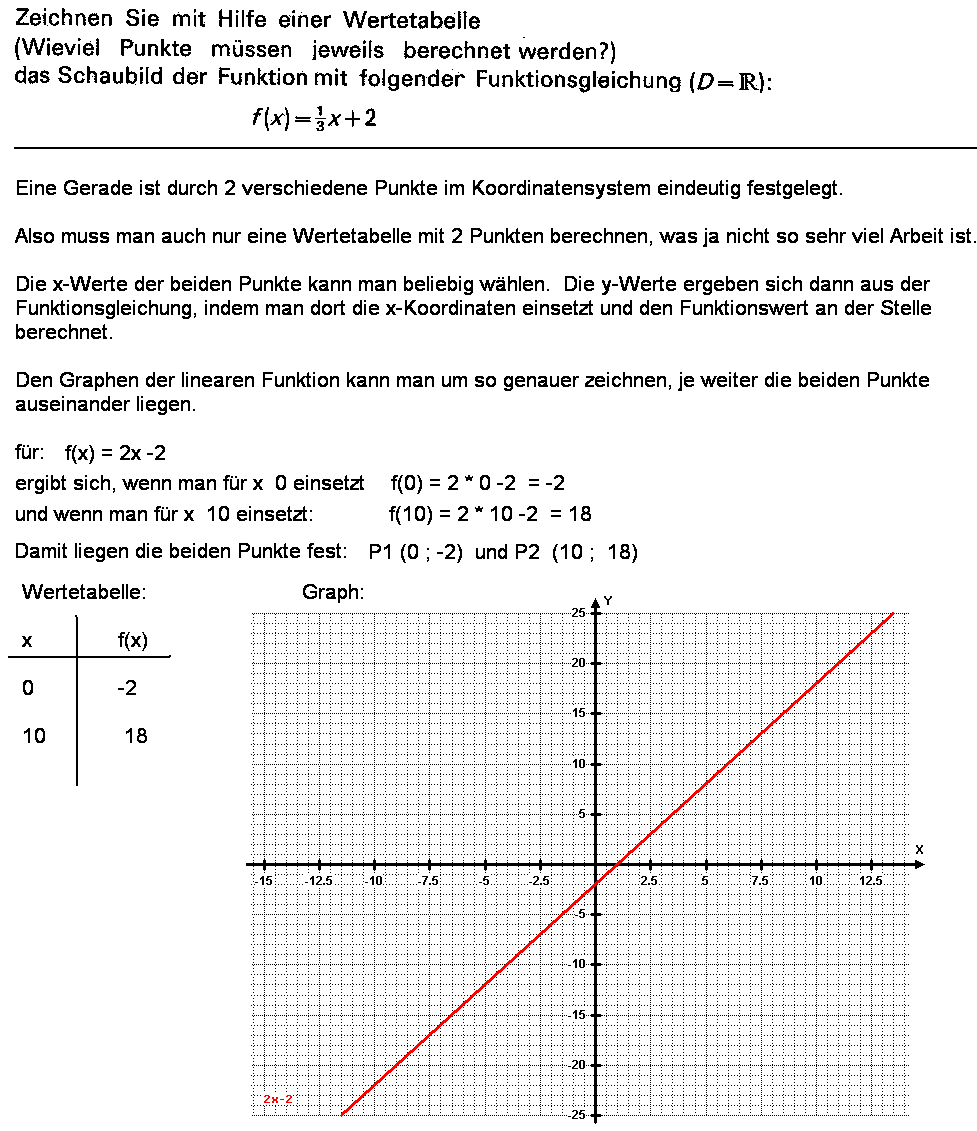
2. Aufgabe | |||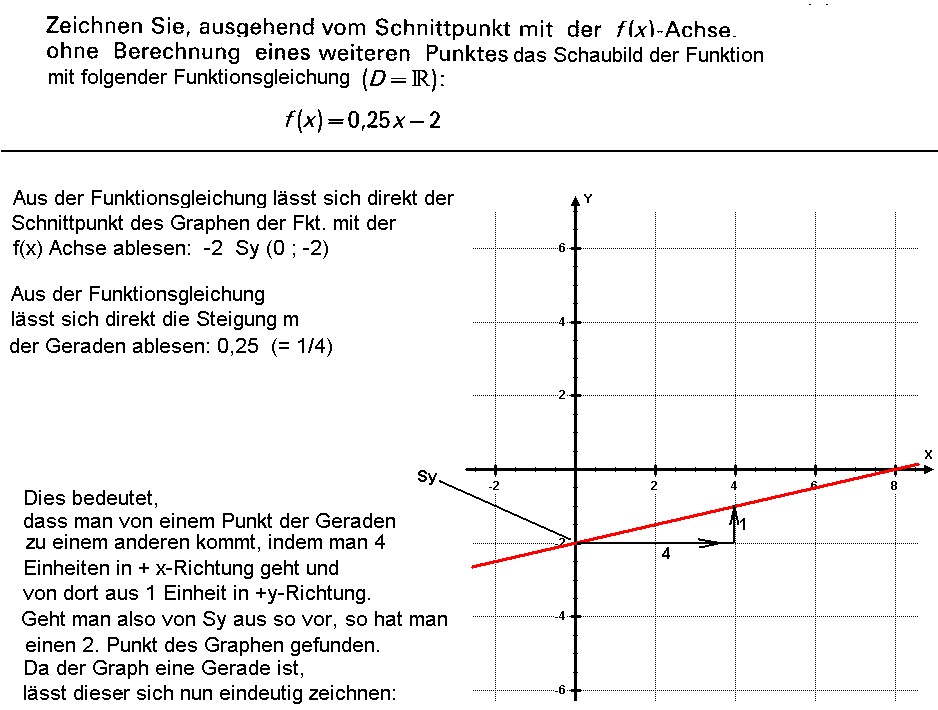
3. Aufgabe | |||
4. Aufgabe | |||
5. Aufgabe | |||
6. Aufgabe | |||
7. Aufgabe | |||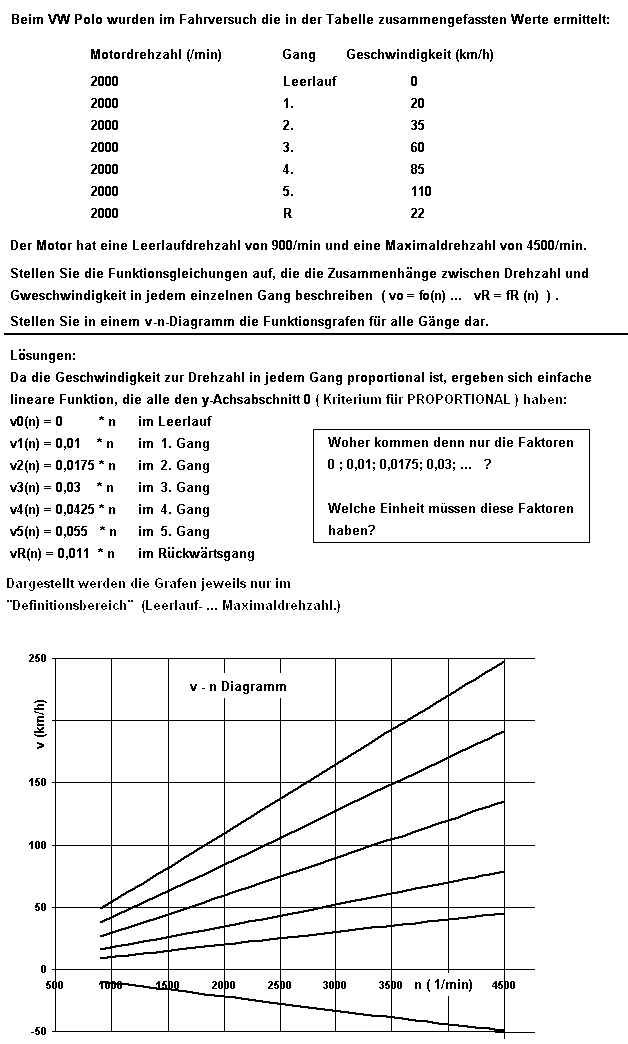
8. Aufgabe | |||
9. Aufgabe | |||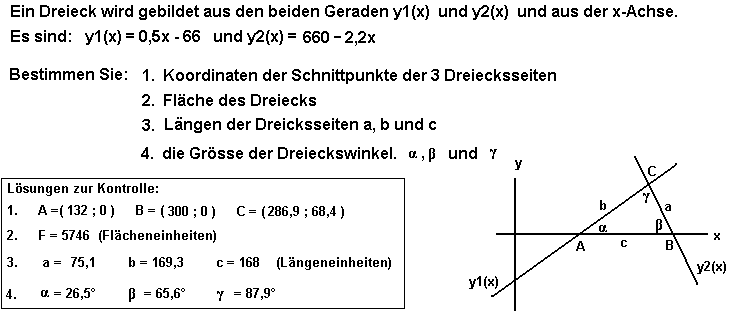
10. Aufgabe | |||
9. Aufgabe
Diese Aufgabe war ein Preisrätsel aus bild der wissenschaft 2/2011.Das Bild zeigt den Kreuzgang und den Innenhof von "Kloster Haftenau" mit seinen Steinlinien und Brunnen. Die roten Bodenlinien verbinden jeweils die Eckpunkte des quadratischen Innenhofs mit den gegenüberliegenden Seitenmitten, so dass sich eine regelmäßige achteckige Innenfläche ergibt. Der Brunnen in der Mitte ist ebenfalls ein regelmäßiges Achteck, dessen Kantenlänge jedoch nur halb so groß ist wie die Kantenlänge des roten Achtecks. Wie viel Prozent der Innenhoffläche nimmt der Brunnen ein? Lösungshinweise: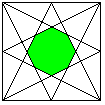 
Der Innenhof von "Kloster Haftenau" schematisch und auf das hier Wesentliche beschränkt.
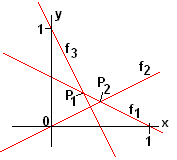3 Bodenlinien wurden hier herausgegriffen und als lineare Funktionen in einem geeigneten Koordinatensystem dargestellt.Da nach prozentualem Anteil gefragt ist, darf die Kantenlänge des Innenhofquadrats mit 1 angenommen werden. Jede andere Kantenlänge tut´s auch. Bei der Prozentberechnung kürzt sich die tatsächliche Kantenlänge wieder heraus. Stelle nun die 3 Gleichungen für die 3 linearen Funktionen f1, f2 und f3 auf. Berechne die Koordinaten der beiden Schnittpunkte P1 und P2. Mit dem Pythagoras kann man nun die Kantenlänge des Linienachtecks berechnen.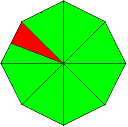 
Kennt man die Kantenlänge eines regelmäßigen Achtecks, lässt sich die zugehörige Fläche auch ermitteln.(Von dem roten Dreieck z.B. sind eine Kantenlänge und die Winkel praktisch bekannt.) Da die Kantenlänge des Brunnenachtecks nur halb so groß ist, wie die des Linienachtecks, ist also die Fläche des Brunnenachtecks nur ..... so groß wie die des Linienachtecks. Lösung : p=4,19%
| 10. Aufgabe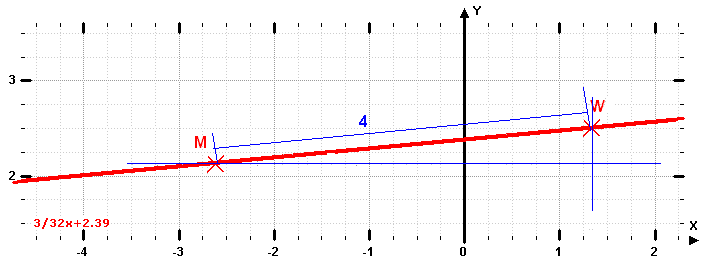
Wie heißen die Koordinaten von Punkt M, der im Abstand von 4 Einheiten links von Punkt W (4/3 ; 68/27) auf der Geraden
g(x) = 3/32x +2,39 liegen soll? Hier hilft Pythagoras: a2 = (XW- XM)2 + (YW - YM)2 In dieser Gleichung sind XM) und YM) unbekannt. Man benötigt also noch eine weitere Gleichung. Es gilt natürlich auch für M die Geradengleichung, da M auf der Geraden liegt: g(XM) = YM = 3/32XM + 2,39 Nutzt man diese Gleichung und setzt YM in den Pythagoras ein, erhält man eine Gleichung mit der Unbekannten XM: a2 = (XW- XM)2 + (YW - (3/32XM + 2,39))2 Durch fleißiges Umformen gelangt man zu der quadratischen Gleichung: u*x2 + v*x + w = 0 mit u = (1 + m2) = 1,0088 und v = -2xw - 2m(yw - b) = 2,6901 und w = xw2 + (yw - b)2 - a2 = -14,2066 Diese quadratische Gleichung löst jeder etwas begabtere Taschenrechner in NULLKOMMANIX: xM1 = 5,3159 xM2 = -2,6492 Da der Punkt M links von W liegen soll, kommt als Lösung nur xM2 in Frage. Die zugehörige y-Koordinate von M erhält man, in dem man den Wert von xM2 in die Geradengleichung g(x) einsetzt: yM2 = 2,1416 Damit lautet die Lösung: Der Punkt M (-2,6492; 2,1416) liegt links von Punkt W auf der Geraden g und hat von W den Abstand 4.Die Probe erfolgt durch Berechnung des Abstands zwischen W und M: a= Wurzel ((xw - xM2)2 + (yw - yM2)2) = ... = 4 Hier finden Sie eine zu dieser Aufgabe passende Excel-Berechnung. |
| www.kszofingen.ch | interaktive Mathetests | www.mathe-online.at | www.ies.co.jp | engl. Mathe-Java-Applets | mathenexus.zum.de | www.arndt-bruenner.de | mathematik.zum.de | www.tutorvista.com | kostenpflichtige Nachhilfe weltweit jederzeit |
 |
vorige Seite nächste Seite |
 email an Autor |
Musterlösungen, Übersicht und Links |
 Autoelektrik Startseite |
Berufskolleg Mitte - Essen |