Seitenende Autoelektrik (Startseite)

Grundlagen der Elektronik


Logische Schaltungen



zuletzt bearbeitet am 1.6.2005 		UND 3 Eingänge

Schaltsymbole Funktionstabellen


Regeln der Schaltalgebra


Schaltungsanalyse


Schaltungssynthese


spezielle Logische Schaltungen






















Elektronische Steuerungssysteme in Fahrzeugen sind üblicherweise digitale Steuerungen.
Eine Grundlage der digitalen Steuerungen bilden die logischen Verknüpfungen. Hierbei handelt es sich um Transistorschaltungen, die ein oder mehrere binäre (Werte 0 oder 1) Eingangssignale miteinander verarbeiten zu einem binären Ausgangssignal. Im Prinzip würde man mit den 3 elementaren Verknüpfungen UND, ODER und NICHT alle gewünschten komplexen logischen Verknüpfungen zusammenstellen können, jedoch bietet die Industrie weitere Grundkomponenten an, um die Gesamtschaltungen zu vereinfachen. Da viele logische Schaltungen (abgesehen von der Energieversorgung) mit 3 Anschlüssen (2 Eingänge, 1 Ausgang) auskommen, werden auf einem IC (integrated circuit) mit z.B. 14 Pins 4 gleichartige Schaltungen untergebracht.4-fach NAND IC SN7400

In diesem Kapitel werden die einzelnen logischen Grundschaltungen und ihre Eigenschaften vorgestellt.
Es wird ein Überblick über die Rechengesetze der formalen Logik gezeigt.
An je einem Beispiel wird dargestellt, wie man das Verhalten einer komplexen logischen Schaltung herausfindet (Schaltungsanalyse).
Schließlich demonstriert ein weiteres Beispiel, wie man eine Schaltung entwickelt, die ein bestimmtes Verhalten zeigen soll (Schaltungssynthese).




Seitenanfang

Schaltsymbole Funktionstabellen

Regeln der Schaltalgebra










Symbol

Funktionstabelle

Gleichung
Schaltalgebra

Bemerkungen
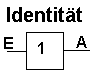
<strong>Identität</strong> Funktionstabellen Identität Formel Schaltalgebra Identität Bei dieser Schaltung (Gleichheit oder Identität) ist das Ausgangssignal gleich dem Eingangssignal.
Die Schaltung hat nur einen Eingang und auch nur einen Ausgang. (Was soll´s???)
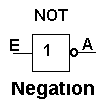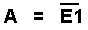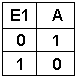
<strong>NOT</strong> Funktionstabellen NOT Formel Schaltalgebra NOT Bei dieser Schaltung (NOT oder NICHT) ist das Ausgangssignal entgegengesetzt zum Eingangssignal.
Die Schaltung invertiert das Eingangssignal.

Der Kreis hinter der Identität-Schaltung bedeutet also die Invertierung des Signals.
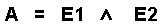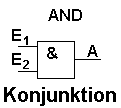
<strong>AND</strong> Funktionstabellen AND Formel Schaltalgebra AND Bei dieser Schaltung (AND oder UND) hat das Ausgangssignal genau dann den Wert 1, wenn der Eingang E1 UND der Eingang E2 den Wert 1 hat.


Der Pfeil nach oben in der Formel bedeutet also UND
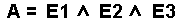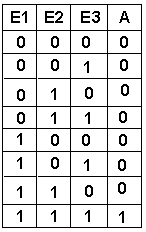
AND 3 Eingänge Funktionstabellen AND 3 Eingänge Formel Schaltalgebra AND 3 Eingänge Bei dieser Schaltung (AND mit 3 Eingängen) hat das Ausgangssignal genau dann den Wert 1, wenn der Eingang E1 UND der Eingang E2 UND der Eingang E3> den Wert 1 hat.
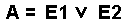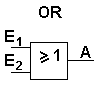
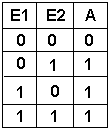
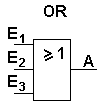
<strong>OR</strong> Funktionstabellen OR Formel Schaltalgebra OR Bei dieser Schaltung (OR oder ODER) hat das Ausgangssignal genau dann den Wert 1, wenn der Eingang E1 ODER der Eingang E2 den Wert 1 hat ODER beide Eingänge haben den Wert 1.


Diese Festlegung ist wichtig, da in der Umgangssprache nicht so deutlich zwischen den beiden verschiedenen ODER unterschieden wird (siehe auch XOR).
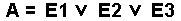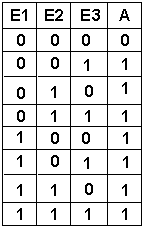
OR 3 Eingänge Funktionstabellen OR 3 Eingänge Formel Schaltalgebra OR 3 Eingänge Bei dieser Schaltung (OR mit 3 Eingängen) hat das Ausgangssignal genau dann den Wert 1, wenn der Eingang E1 ODER der Eingang E2 ODER der Eingang E3> den Wert 1 hat ODER 2 Eingänge den Wert den 1 haben ODER sogar alle 3 Eingänge den Wert 1 haben.


Man kann es auch einfacher ausdrücken:

Bei dieser Schaltung hat der Ausgang nur dann den Wert 0, wenn alle Eingänge den Wert 0 haben.
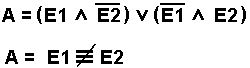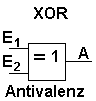
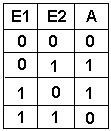
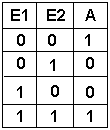
<strong>XOR</strong> Funktionstabellen XOR Formel Schaltalgebra XOR Bei dieser Schaltung (XOR oder Exclusiv-ODER oder Antivalenz ) hat das Ausgangssignal genau dann den Wert 1, wenn genau einer der beiden Eingänge E1 ODER E2 den Wert 1 hat. Wenn beide Eingänge den Wert 1 haben, ist der Ausgang 0. (vergleiche mit OR).

Diese Schaltung ist keine Grundschaltung mehr, sondern muss aus mehreren Basisschaltungen kombiniert werden.

Die obere Formel für diese Schaltung zeigt, welche Basisschaltungen erforderlich sind.
Der Balken über den Zeichen E1 bzw. E2 bedeutet NICHT-E1 bzw. NICHT E2.

Damit entsprechen diese Balken in der Formel dem Kreiszeichen im Schaltsymbol.

Das Symbol in der unteren Gleichung zwischen E1 und E2 bedeutet nicht äquivalent.
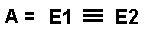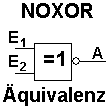
<strong>NOXOR</strong> Funktionstabellen NOXOR Formel Schaltalgebra NOXOR Bei dieser Schaltung (NOXOR oder Äquivalenz) hat das Ausgangssignal genau dann den Wert 1, wenn beiden Eingänge E1 und E2 den Wert 1 haben oder wenn beide Eingänge den Wert 0 haben.

Auch diese Schaltung ist keine Grundschaltung mehr. Sie muss aus mehreren Basisschaltungen kombiniert werden.

Das Symbol in der Gleichung zwischen E1 und E2 bedeutet äquivalent.
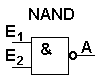
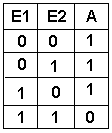
<strong>NAND</strong> Funktionstabellen NAND Formel Schaltalgebra NAND Bei dieser Schaltung (NAND oder NICHT-UND) hat das Ausgangssignal genau die entgegengesetzten Werte wie die NAND-Schaltung.

Der Ausgang der UND-Schaltung wird noch invertiert.

Der lange Balken in der Formel bedeutet, dass zunächst die normale AND-Verknüpfung erfolgt und anschließend das Ergebnis invertiert wird.
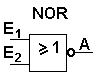
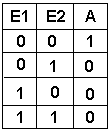
<strong>NOR</strong> Funktionstabellen NOR Formel Schaltalgebra NOR Bei dieser Schaltung (NOR oder NICHT-ODER) hat das Ausgangssignal genau die entgegengesetzten Werte wie die OR-Schaltung.

Der Ausgang der OR-Schaltung wird noch invertiert.
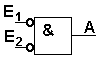
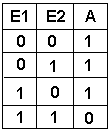
UND mit 2 invertierten Eingängen Funktionstabellen UND mit 2 invertierten Eingängen Formel Schaltalgebra UND mit 2 invertierten Eingängen Bei dieser Schaltung (UND mit 2 invertierten Eingängen) ist das Ausgangssignal völlig anders als bei der NAND-Schaltung!

Hier wird zunächst jedes Eingangssignal invertiert und diese beiden Signale dann mit AND verknüpft.
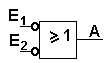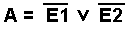OR mit 2 invertierten Eingängen Funktionstabellen OR mit 2 invertierten Eingängen Formel Schaltalgebra OR mit 2 invertierten Eingängen Bei dieser Schaltung (OR mit 2 invertierten Eingängen) ist das Ausgangssignal völlig anders als bei der NOR-Schaltung!





Schaltsymbole Funktionstabellen

Regeln der Schaltalgebra

Schaltungsanalyse










Bezeichnung

Rechengesetz

Bemerkungen

Umkehrregel
oder
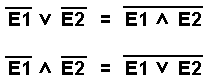de Morgansche Regel

 de Morgansche Regel Damit kann man die NAND-Schaltung ersetzen durch eine OR-Schaltung mit 2 invertierten Eingängen.

Damit kann man die NOR-Schaltung ersetzen durch eine AND-Schaltung mit 2 invertierten Eingängen.

Konjunktion

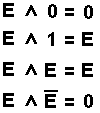 Konjunktion

Disjunktion

 Disjunktion

Negation

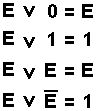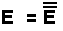 Negation Durch doppelte Negation erhält man wieder den Ursprungswert

Vertauschungsgesetz
oder
Kommutationsgesetz

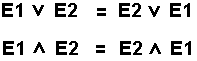 Kommutationgesetz

Verteilungsgesetz
oder
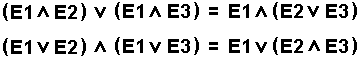Distributionsgesetz

 Distributionsgesetz

Idempotenzgesetz

 Idempotenzgesetz 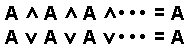Tritt eine Variable mehrfach auf, so darf sie bis auf eine gestrichen werden.
Die gleiche Variable darf beliebig oft als UND- oder ODER- Verknüpfung hinzugefügt werden.

Absorptionsregeln

 Absorptionsregeln





Mit diesen Gesetzen und Regeln kann man zeigen, dass man allein mit NAND- oder allein mit NOR-Verknüpfungen die drei Grundverknüpfungen AND, OR und NOT erzeugen kann.



Da außerdem AND, OR und NOT ausreichen, um alle komplexen logischen Verknüpfungen darzustellen, kann man das also auch nur mit jeder der beiden Schaltungen NAND oder NOR.

Regeln der Schaltalgebra

Schaltungsanalyse

Schaltungssynthese










Bei der Schaltungsanalyse geht es darum, die Funktionstabelle zu einer gegebenen logischen Schaltung zu erstellen.


Das ist nicht schwierig, kann jedoch recht umfangreich werden.
Man beginnt die Wahrheitstabelle wie immer mit allen Zustandsmöglichkeiten der Eingänge, die man systematisch in den ersten Spalten der Tabelle notiert.
Die letzte Spalte bleibt für den Ausgang reserviert.
Je nach Komplexität der Schaltung empfiehlt es sich, einige Zwischenspalten für Zwischenzustände zu notieren.
Dies soll nun an folgendem Beispiel demonstriert werden:


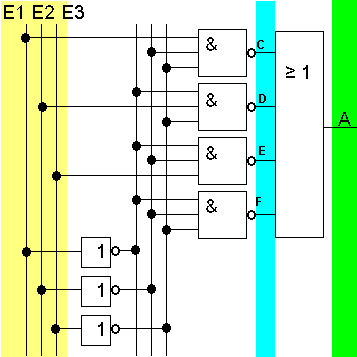Beispiel für komplexe logische Schaltung Diese Schaltung besteht also aus 3 Invertern (NOT), 4 NAND- und einer OR-Schaltung.
Sie hat 3 Eingänge, die jeweils den Wert 0 bzw. 1 annehmen können.
Damit muss die Funktionstabelle außer der Kopfzeile, 8 Zeilen haben.
Sie benötigt weiterhin mindestens 4 Spalten, für jeden Eingang eine und für den Ausgang eine.
Hilfreich sind 4 Zusatzspalten für die Eingänge der OR-Schaltung C, D, E und F.

Damit sieht die vorbereitete Tabelle so aus:

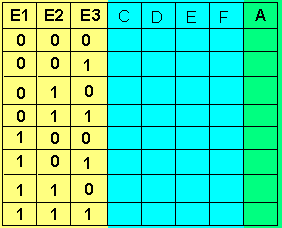Leertabelle Der Wert C ergibt sich aus:
Nicht-(E1 UND Nicht-E2 UND Nicht E3).

Entsprechend erbibt sich der Wert von D aus:
Nicht-(Nicht-E1 UND E2 UND Nicht-E3),

der Wert von E aus:
Nicht-(Nicht-E1 UND Nicht-E2 UND E3),

und schließlich der Wert für F aus:
Nicht-(Nicht-E1 UND Nicht-E2 UND Nicht-E3).








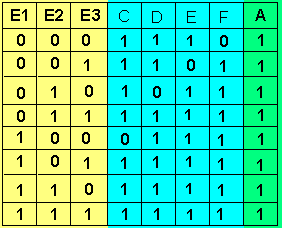Funktionstabelle Die fertige Funktionstabelle zeigt die Abbildung rechts.

Die zu der Schaltung passenden Gleichungen zeigt das Bild unten:

Gleichung Schaltalgebra














Diese Schaltung ist natürlich ohne jeden Nutzen, da unabhängig von den Eingangsstellungen das Ausgangssignal stets 1 ergibt.

Schaltungsanalyse

Schaltungssynthese

spezielle Logische Schaltungen






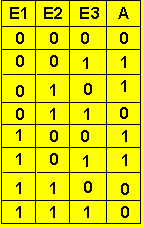
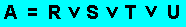
Funktionstabelle

Bei der Schaltungssynthese geht es darum, für eine gegebene Funktionstabelle die passende logischen Schaltung zu entwerfen.


Dieser Fall ist der Normalfall, da meist eine vorgegebene Steuerungsfunktion durch eine logische Schaltung realisiert werden soll.
Eine mögliche Vorgehensweise soll hier für die rechts abgebildete Funktionstabelle beispielhaft vorgeführt werden.

In 4 von 8 Fällen ist der Wert des Ausgangs 1, sonst 0. Wenn man diese 4 Fälle jeweils mit R, S, T und U bezeichnet, so kann man eine einfache Gleichung aufstellen: Funktionstabelle

Und damit ist klar, dass das letze logische Glied in der Gesamtschaltung eine OR-Schaltung mit 4 Eingängen sein muss.

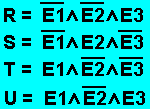EinzelfallGleichungen Nun gilt es noch 4 Einzelgleichungen für die Fälle R, S, T und U aufzustellen und dann alles miteinander zu kombinieren.

R = Nicht-E1 UND Nicht-E2 UND E3
S = Nicht-E1 UND E2 UND Nicht-E3
T = E1 UND Nicht-E2 UND Nicht-E3
U = E1 UND Nicht-E2 UND E3


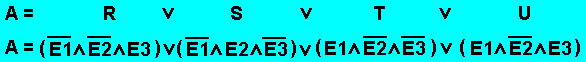Gesamtgleichungen Diese 4 Fälle werden nun noch mit ODER verknüpft, und





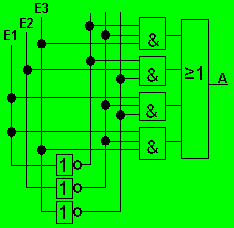nicht optimierte logische Schaltung die Gleichung wird durch entsprechende Logikkomponenten nachgebildet.


Die rechts abgebildete Schaltung erfüllt die Bedingungen der gegebenen Wahrheitstabelle.









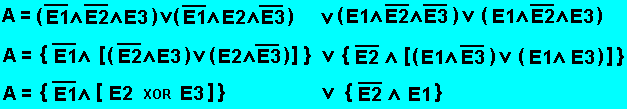Gleichungsumformung Durch geschicktes Ausnutzen der Rechenregeln lässt sich die Gleichung jedoch umformen.
In der 1. Umformung wurde das Distributionsgesetz ausgenutzt.
In der 2. Umformung wurde sowohl die XOR-Schaltgleichung genutzt als auch die das Distributionsgesetz und die Disjunktion.

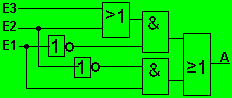optimierte Schaltung In diesem Fall kann man dadurch Bauteile (und Geld und Arbeit) sparen:

Die rechts abgebildete optimierte Schaltung hat dasselbe Schaltverhalten wie die aufwendigere nicht optimierte Schaltung.














Schaltungssynthese

spezielle Logische Schaltungen

Seitenende















Die Seite www.realschule.bayern zeigt jede Menge gut verständliche Informationen zum Thema Logische Schaltungen.

Zur Simulation der Schaltungen eignet sich die für Schüler und Studenten kostenlos downloadbare Software CircuitMaker (ist jedoch auf englisch! und natürlich nicht mit den ISO- sondern mit den ANSI-Schaltsymbolen )


















Seitenanfang Quickstart eMail an Autor Startseite zurückblättern vorblättern Stichwortverzeichnis Aufgaben Seite:

40